【题目】函数y=ex﹣mx在区间（0，3]上有两个零点，则m的取值范围是 ．
【答案】e＜m≤ 
【解析】解：由y=ex﹣mx=0得m= 
，
设f（x）= ，
则f'（x）= 
，
由f'（x）＞0，解得1＜x≤3，此时函数单调递增，
由f'（x）＜0，解得0＜x＜1，此时函数单调递减，
∴当x=1时，函数f（x）取得极小值，同时也是最小值f（1）=e，
∵当x→0时，f（x）→+∞，
当x=3时，f（3）= ，
∴要使函数y=ex﹣mx在区间（0，3]上有两个零点，
则e＜m≤ ，
所以答案是：e＜m≤ ．
【考点精析】本题主要考查了函数的零点的相关知识点，需要掌握函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点才能正确解答此题．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某学生对其30位亲属的饮食习惯进行了一次调查,并用如图所示的茎叶图表示他们的饮食指数(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主).
(1)根据茎叶图,帮助这位同学说明这30位亲属的饮食习惯.
(2)根据以上数据完成如下2×2列联表.
(3)能否有99％的把握认为其亲属的饮食习惯与年龄有关?
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.a∈R，“ 
＜1”是“a＞1”的必要不充分条件
B.“p∧q为真命题”是“p∨q为真命题”的必要不充分条件
C.命题“?x∈R使得x2+2x+3＜0”的否定是：“?x∈R，x2+2x+3＞0”
D.命题p：“?x∈R，sinx+cosx≤ 
”，则￢p是真命题
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和Sn=kcn﹣k（其中c，k为常数），且a2=4，a6=8a3 ．
（1）求an；
（2）求数列{nan}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分
分）
如图
，在
中， 
， 
， 
分别为
， 
的中点，点
为线段
上的一点，将
沿
折起到
的位置，使
，如图
．
（Ⅰ）求证： 
平面
．
（Ⅱ）求证： 
．
（Ⅲ）线段
上是否存在点
，使
平面
？说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，平面
平面
，四边形
为矩形， 
，点
为
的中点.
(1)证明： 
平面
.
(2)点
为
上任意一点，在线段
上是否存在点
，使得
？若存在，确定点
的位置，并加以证明；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且cos2 
﹣sinBsinC= 
．
（1）求A；
（2）若a=4，求△ABC面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题共13分）
以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊，无法确认，在图中经X表示。
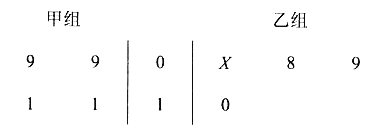
（Ⅰ）如果X=8，求乙组同学植树棵数的平均数和方差；
（Ⅱ）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率。
（注：方差
其中
为
，
，
的平均数）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
