
【题目】已知函数![]() . 设关于
. 设关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是___.
的取值范围是___.
【答案】![]()
【解析】
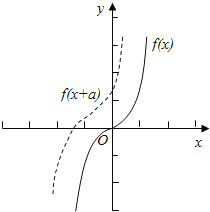
由题意可得,在[![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.当a=0或 a>0时,检验不满足条件.当a<0时,应有f(![]() a)<f(
a)<f(![]() ),化简可得 a2﹣a﹣1<0,由此求得a的范围.
),化简可得 a2﹣a﹣1<0,由此求得a的范围.
由于f(x)![]() ,
,
关于x的不等式f(x+a)<f(x)的解集为M,若[![]() ,
,![]() ]A,
]A,
则在[![]() ,
,![]() ]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
]上,函数y=f(x+a)的图象应在函数y=f(x)的图象的下方.
当a=0时,显然不满足条件.
当a>0时,函数y=f(x+a)的图象是把函数y=f(x)的图象向左平移a个单位得到的,
结合图象(右上方)可得不满足函数y=f(x+a)的图象在函数y=f(x)的图象下方.
当a<0时,如图所示,要使在[![]() ,
,![]() ]上,
]上,
函数y=f(x+a)的图象在函数y=f(x)的图象的下方,
只要f(![]() a)<f(
a)<f(![]() )即可,
)即可,
即﹣a(![]() a)2+(
a)2+(![]() a)<﹣a(
a)<﹣a(![]() )2
)2![]() ,
,
化简可得 a2﹣a﹣1<0,解得 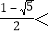 a
a![]() ,
,
故此时a的范围为(![]() ,0).
,0).
综上可得,a的范围为(![]() ,0),
,0),
故答案为:(![]() ,0).
,0).


科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用![]() ,
,![]() ,
,![]() ,
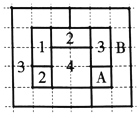
,![]() 四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为
四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为![]() ,粗实线围城的各区域上分别标有数字
,粗实线围城的各区域上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的四色地图符合四色定理,区域
的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为![]() 的区域的概率所有可能值中,最大的是( )
的区域的概率所有可能值中,最大的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
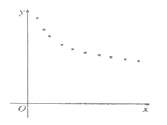
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为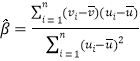 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式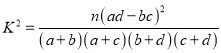 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程。
已知曲线C![]() :
:![]() (t为参数), C
(t为参数), C![]() :
:![]() (
(![]() 为参数)。
为参数)。
(1)化C![]() ,C
,C![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C![]() 上的点P对应的参数为
上的点P对应的参数为![]() ,Q为C
,Q为C![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线
![]() (t为参数)距离的最小值。
(t为参数)距离的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC=4,点B(-1,3),点C(4,-2),且其“欧拉线”与圆M:![]() 相切,则下列结论正确的是( )
相切,则下列结论正确的是( )
A.圆M上点到直线![]() 的最小距离为2
的最小距离为2![]()
B.圆M上点到直线![]() 的最大距离为3
的最大距离为3![]()
C.若点(x,y)在圆M上,则![]() 的最小值是
的最小值是![]()
D.圆![]() 与圆M有公共点,则a的取值范围是
与圆M有公共点,则a的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AD.M,N分别是AB,PC的中点.
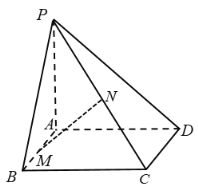
(1)求证:MN//平面PAD;
(2)求证:MN⊥平面PCD;
(3)求二面角B—PC—D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com