
【题目】已知函数f(x)=aex﹣x(a∈R),其中e为自然对数的底数,e=2.71828…
(Ⅰ)判断函数f(x)的单调性,并说明理由
(Ⅱ)若x∈[1,2],不等式f(x)≥e﹣x恒成立,求a的取值范围.
【答案】解:(Ⅰ)由f(x)=aex﹣x,得f′(x)=aex﹣1, 当a≤0时,f′(x)<0,f(x)=aex﹣x为R上的减函数;
当a>0时,令aex﹣1=0,得x=lna,
若x∈(﹣∞,﹣lna),则f′(x)<0,此时f(x)为的单调减函数;
若x∈(﹣lna,+∞),则f′(x)>0,此时f(x)为的单调增函数.
综上所述,当a≤0时,f(x)=aex﹣x为R上的减函数;
当a>0时,若x∈(﹣∞,﹣lna),f(x)为的单调减函数;
若x∈(﹣lna,+∞),f(x)为的单调增函数.
(Ⅱ)由题意,x∈[1,2],不等式f(x)≥e﹣x恒成立,等价于aex﹣x≥e﹣x恒成立,
即x∈[1,2], ![]() 恒成立.
恒成立.
令g(x)= ![]() ,则问题等价于a不小于函数g(x)在[1,2]上的最大值.
,则问题等价于a不小于函数g(x)在[1,2]上的最大值.
由g(x)= ![]() =
= ![]() ,函数y=
,函数y= ![]() 在[1,2]上单调递减,
在[1,2]上单调递减,
令h(x)= ![]() ,x∈[1,2],h′(x)=
,x∈[1,2],h′(x)= ![]() .
.
∴h(x)= ![]() 在x∈[1,2]上也是减函数,
在x∈[1,2]上也是减函数,
∴g(x)在x∈[1,2]上也是减函数,
∴g(x)在[1,2]上的最大值为g(1)= ![]() .
.
故x∈[1,2],不等式f(x)≥e﹣x恒成立的实数a的取值范围是[ ![]() ,+∞).
,+∞).
【解析】(Ⅰ)求出原函数的导函数,然后对a分类,当a≤0时,f′(x)<0,f(x)=aex﹣x为R上的减函数;当a>0时,由导函数为0求得导函数的零点,再由导函数的零点对定义域分段,根据导函数在各区间段内的符号得到原函数的单调性;(Ⅱ)x∈[1,2],不等式f(x)≥e﹣x恒成立,等价于aex﹣x≥e﹣x恒成立,分离参数a,可得 ![]() 恒成立.令g(x)=
恒成立.令g(x)= ![]() ,则问题等价于a不小于函数g(x)在[1,2]上的最大值,然后利用导数求得函数g(x)在[1,2]上的最大值得答案.
,则问题等价于a不小于函数g(x)在[1,2]上的最大值,然后利用导数求得函数g(x)在[1,2]上的最大值得答案.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】2017年春晚分会场之一是凉山西昌,电视播出后,通过网络对凉山分会场的表演进行了调查.调查分三类人群进行,参加了网络调查的观众们的看法情况如下:
观众对凉山分会场表演的看法 | 非常好 | 好 |
中国人且非四川(人数比例) |
|
|
四川人(非凉山)(人数比例) |
|
|
凉山人(人数比例) |
|
|
(1)从这三类人群中各选一个人,求恰好有2人认为“非常好”的概率(用比例作为相应概率);
(2)若在四川人(非凉山)群中按所持态度分层抽样,抽取9人,在这9人中任意选取3人,认为“非常好”的人数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元. 在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
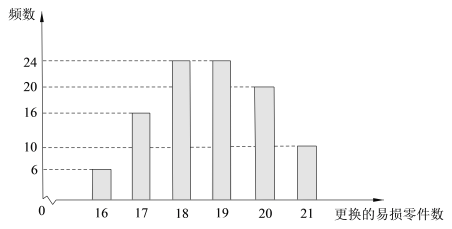
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(1)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(2)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的最小值;
的最小值;
(3)假设这100台机器在购机的同时每台都购买18个易损零件,或每台都购买19个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买18个还是19个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,2acosC=bcosC+ccosB.
(1)求角C的大小;
(2)若c=![]() ,a2+b2=10,求△ABC的面积.
,a2+b2=10,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:
年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅰ)求身高y关于年龄x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:![]() =
=  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足:Sn=nan﹣2n(n﹣1),首项![]() =1.
=1.
(1)求数列{an}的通项公式;
(2)设数列![]() 的前n项和为Mn,求证:
的前n项和为Mn,求证:![]()
![]() Mn
Mn![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为双曲线
分别为双曲线![]() 的左、右顶点,双曲线的实轴长为
的左、右顶点,双曲线的实轴长为![]() ,焦点到渐近线的距离为
,焦点到渐近线的距离为![]() .
.
(1)求双曲线的方程;
(2)已知直线![]() 与双曲线的右支交于
与双曲线的右支交于![]() 两点,且在双曲线的右支上存在点
两点,且在双曲线的右支上存在点![]() ,使
,使![]() ,求
,求![]() 的值及点
的值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+cosωx(ω>0),x∈R,若函数f(x)在区间(﹣ω,ω)内单调递增,且函数y=f(x)的图象关于直线x=ω对称,则ω的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 的斜率分别记为
的斜率分别记为![]() 与
与![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 的面积是否存在最大值?若存在,求出
的面积是否存在最大值?若存在,求出![]() 面积的最大值;若不存在,请说明理由.
面积的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com