
【题目】如图,正三棱柱ABCA1B1C1的所有棱长都为2,D为CC1的中点.

(1)求证:AB1⊥平面A1BD;
(2)求二面角AA1DB的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)通过建立如图所示的空间直角坐标系,利用数量积![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
(2)利用两个平面的法向量的夹角余弦值即可得到二面角的余弦值.
(1)证明:如图,取BC的中点O,连接AO.

因为△ABC为正三角形,所以AO⊥BC.
因为在正三棱柱ABCA1B1C1中,平面ABC⊥平面BCC1B1,所以AO⊥平面BCC1B1.
取B1C1中点O1,以O为原点,![]() ,
,![]() ,
,![]() 的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,
的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系,
则B(1,0,0),D(-1,1,0),A1(0,2,![]() ),A(0,0,
),A(0,0,![]() ),B1(1,2,0),C(-1,0,0),
),B1(1,2,0),C(-1,0,0),
所以![]() =(1,2,-
=(1,2,-![]() ),
),![]() =(-2,1,0),
=(-2,1,0),![]() =(-1,2,
=(-1,2,![]() ).
).
因为![]() ·
·![]() =-2+2+0=0,
=-2+2+0=0,![]() ·
·![]() =-1+4-3=0,
=-1+4-3=0,
所以![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,即AB1⊥BD,AB1⊥BA1.
,即AB1⊥BD,AB1⊥BA1.
又BD与BA1交于点B,所以AB1⊥平面A1BD.
(2)解:连接AD,设平面A1AD的法向量为
n=(x,y,z).
![]() =(-1,1,-
=(-1,1,-![]() ),
),![]() =(0,2,0).
=(0,2,0).
因为n⊥![]() ,n⊥
,n⊥![]() ,所以
,所以
即![]() 解得
解得![]()
令z=1,得n=(-![]() ,0,1)为平面A1AD的一个法向量.
,0,1)为平面A1AD的一个法向量.
由(1)知AB1⊥平面A1BD,所以![]() 为平面A1BD的法向量.
为平面A1BD的法向量.
cos〈n·![]() 〉=
〉=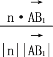 =
=![]() =-
=-![]() ,
,
故二面角AA1DB的余弦值为![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac= ![]() (a2﹣b2﹣c2).(13分)
(a2﹣b2﹣c2).(13分)
(Ⅰ)求cosA的值;
(Ⅱ)求sin(2B﹣A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要制作一个容积为2π m3的圆柱形储油罐(有盖),为使所用的材料最省,它的底面半径与高分别为 ( )
A. 0.5 m,1 m B. 1 m,1 m
C. 1 m,2 m D. 2 m,2 m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在创建全国旅游城市的活动中,对一块以O为圆心,R(R为常数,单位:米)为半径的半圆形荒地进行治理改造,其中弓形BCD区域(阴影部分)种植草坪,△OBD区域用于儿童乐园出租,其余区域用于种植观赏植物.已知种植草坪和观赏植物的成本分别是每平方米5元和55元,儿童乐园出租的利润是每平方米95元.
(1)设∠BOD=θ(单位:弧度),用θ表示弓形BCD的面积S弓=f(θ).
(2)如果该市规划办邀请你规划这块土地,如何设计∠BOD的大小才能使总利润最大?并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=alnx+ ![]() +
+ ![]() x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com