练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等差数列{an}中，公差d=1，s98=137，则a2+a4+a6+…+a98等于（ ）
    A．91
    B．92
    C．93
    D．94
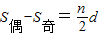
    【答案】分析：当等差数列的项数n为偶数时，则有，Sn=S奇+S偶，进而可以得到答案．
    解答：解：设前98项中，所有奇数项的和为S奇，所有偶数项的和为S偶，（各有49项）
    所有s98=S奇+S偶=137，
    又因为S偶-S奇=49d，且d=1，
    所以S偶-S奇=49d=49，
    所以a2+a4+a6+…+a98=S偶=93．
    故选C．
    点评：解决此类问题的关键是熟练掌握等差数列的有关性质，并且结合正确的运算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案