
【题目】【2017届云南曲靖一中高三文上学期月考四】已知函数![]() .
.
(1)若![]() 是
是![]() 的极值点,求
的极值点,求![]() 的极大值;
的极大值;
(2)求![]() 的范围,使得
的范围,使得![]() 恒成立.
恒成立.
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】某家用电器公司生产一新款热水器,首先每年需要固定投入 200万元,其次每生产1百台,需再投入0.9万元.假设该公司生产的该款热水器当年能全部售出,但每销售1百台需另付运输费0.1万元.根据以往的经验,年销售总额![]() (万元)关于年产量
(万元)关于年产量![]() (百台)的函数为
(百台)的函数为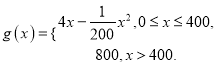 .
.
(1)将年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)求该公司生产的该款热水器的最大年利润及相应的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
注:地震强度是指地震时释放的能量.
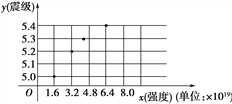
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图(如图)可知a的值等于________.(取lg 2=0.3进行计算)
查看答案和解析>>
科目:高中数学 来源: 题型:
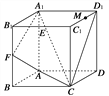
【题目】如图,在正方形ABCD-A1B1C1D1中,E,F,M分别是棱B1C1,BB1,C1D1的中点,是否存在过点E,M且与平面A1FC平行的平面?若存在,请作出并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司试销一种成本单价为500元的新产品,规定试销时销售单价不低于成本单价,又不高于800元.经试销调查,发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y=kx+b(k≠0),函数图象如图所示.

(1)根据图象,求一次函数y=kx+b(k≠0)的表达式;
(2)设公司获得的毛利润(毛利润=销售总价-成本总价)为S元.试问销售单价定为多少时,该公司可获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在“十一”黄金周期间降价搞促销,某超市对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不予优惠;(2)如果超过200元,但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其中500元按第(2)条给予优惠,超过500元的部分给予7折优惠。小张两次去购物,分别付款168元和423元,假设她一次性购买上述同样的商品,则应付款额为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点.若点
两点.若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com