
【题目】如图,四棱锥![]() 的底面
的底面![]() 是菱形,
是菱形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 是等边三角形.
是等边三角形.
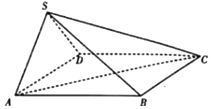
(1)求证:![]() ;
;
(2)若![]() 的面积为
的面积为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
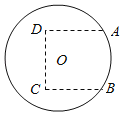
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》中给出了勾股定理的绝妙证明.如图是赵爽弦图及注文.弦图是一个以勾股形之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成朱色及黄色,其面积称为朱实、黄实.由2×勾×股+(股-勾)2=4×朱实+黄实=弦实,化简得勾2+股2=弦2.若图中勾股形的勾股比为![]() ,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:
,向弦图内随机抛掷100颗图钉(大小忽略不计),则落在黄色图形内的图钉颗数大约为( )(参考数据:![]() ,
,![]() )
)
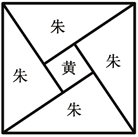
A.2B.4C.6D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,两腰
中,两腰![]() ,底边
,底边![]() 是
是![]() 的三等分点,
的三等分点,![]() 是
是![]() 的中点.分别沿
的中点.分别沿![]() 将四边形
将四边形![]() 和
和![]() 折起,使
折起,使![]() 重合于点
重合于点![]() ,得到如图2所示的几何体.在图2中,
,得到如图2所示的几何体.在图2中,![]() 分别为
分别为![]() 的中点.
的中点.
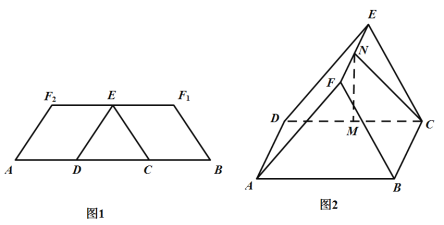
(1)证明:![]() 平面
平面![]()
(2)求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线
上各点纵坐标伸长到原来的2倍(横坐标不变)得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() ,
,![]() (以上两点坐标均为极坐标,
(以上两点坐标均为极坐标,![]() ,
,![]() ),使点
),使点![]() 、
、![]() 到
到![]() 的距离都为3?若存在,求
的距离都为3?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.现分别沿
的中点.现分别沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,点
折起,点![]() 折至点
折至点![]() ,点
,点![]() 折至点
折至点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图2.
,如图2.

(Ⅰ)若![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求多面体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com