
【题目】已知函数![]() .
.
(1)当![]() 时,探究
时,探究![]() 零点的个数;
零点的个数;
(2)①证明:![]() ;
;
②当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)见解析;(2)①见证明;②见证明
【解析】
(1)利用导函数对a进行讨论判断即可.
(2)①对所证函数化简,即证明![]() ,利用导函数研究其单调性,求解最值问题即可证明;②用(1)的结论,求出零点
,利用导函数研究其单调性,求解最值问题即可证明;②用(1)的结论,求出零点![]() ,得出单调性,计算最值
,得出单调性,计算最值![]() ,然后用
,然后用![]() 进行替换,然后用
进行替换,然后用![]() 去掉
去掉![]() ,转化为关于
,转化为关于![]() 的一次式,代入
的一次式,代入![]() 即可证明.
即可证明.
(1)解:![]() ,定义域为
,定义域为![]() .
.
二次函数![]() 的判别式为
的判别式为![]() ,对称轴为
,对称轴为![]() .
.
当![]() 时,二次函数
时,二次函数![]() 的图像开口向下,判别式为
的图像开口向下,判别式为![]() ,
,
所以![]() 在
在![]() 上有1个零点;
上有1个零点;
当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,二次函数
时,二次函数![]() 的图像开口向上,
的图像开口向上,
①![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
②![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上有1个零点
上有1个零点![]() ;
;
③![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上有2个不同的零点;
上有2个不同的零点;
综上,当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() 在
在![]() 上有1个零点;
上有1个零点;
当![]() 时,
时,![]() 在
在![]() 上有2个不同的零点;
上有2个不同的零点;
(2)①要证明:![]() ,只需要证明:
,只需要证明:![]() .
.
令![]() ,定义域为
,定义域为![]() ,
,![]() ,
,
所以![]() ,不难得到
,不难得到![]() 的最大值为
的最大值为![]() ,所以
,所以![]() 成立;
成立;
②由(1)得,当![]() 时,
时,![]() 在
在![]() 上有1个零点;设零点为
上有1个零点;设零点为![]() ,
,
则![]() ,解得,
,解得,![]() ,
,
进一步,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]()
![]() (※)
(※)
由(2)①得,
(※)![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】某校的1000名高三学生参加四门学科的选拔考试,每门试卷共有10道题,每题10分,规定:每门错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,在录取时,
,在录取时,![]() 记为90分,
记为90分,![]() 记为80分,
记为80分,![]() 记为60分,
记为60分,![]() 记为50分.
记为50分.
根据模拟成绩,每一门都有如下统计表:
答错 题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 90 | 100 | 150 | 150 | 200 | 100 | 100 | 50 | 49 | 1 |
已知选拔性考试成绩与模拟成绩基本吻合.
(1)设![]() 为高三学生一门学科的得分,求
为高三学生一门学科的得分,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)预测考生4门总分为320概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
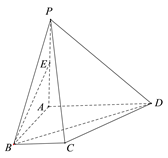
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在R上的偶函数且以2为周期,则“
是定义在R上的偶函数且以2为周期,则“![]() 为
为![]() 上的增函数”是“
上的增函数”是“![]() 为
为![]() 上的减函数”的
上的减函数”的![]()
![]()
A. 充分而不必要的条件B. 必要而不充分的条件
C. 充要条件D. 既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分) 已知双曲线![]() 的两个焦点为
的两个焦点为![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com