练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四棱锥中，底面ABCD为菱形，，侧面为等腰直角三角形，，，点E为棱AD的中点．

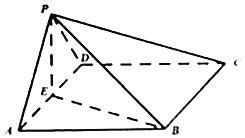
    （1）求证：平面ABCD；

    （2）求直线AB与平面PBC所成角的正弦值．

    【答案】(1)证明见解析，(2)

    【解析】

    （1）题中易得，，利用勾股定理可得，从而可证得线面垂直；

    （2）以E为原点，EA为x轴，EB为y轴，EP为z轴，建立空间直角坐标系，用空间向量法求线面角的正弦值．

    （1）证明：在四棱锥中，底面ABCD为菱形，，

    侧面为等腰直角三角形，，，点E为棱AD的中点．

    ，，，，

    ，，

    ，平面ABCD．

    （2）以E为原点，EA为x轴，EB为y轴，EP为z轴，建立空间直角坐标系，

    0，，，0，，，

    ，，，

    设平面PBC的法向量y，，

    则，取，得1，，

    设直线AB与平面PBC所成角为，

    直线AB与平面PBC所成角的正弦值为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在侧棱垂直于底面的三棱柱中，，，为侧面的对角线的交点，，分别是，中点

    （1）求证：平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）当时，求的极值；

    （2）若有2个不同零点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小区为了提高小区内人员的读书兴趣，特举办读书活动，准备进一定量的书籍丰富小区图书站，由于不同年龄段需要看不同类型的书籍，为了合理配备资源，现对小区看书人员进行年龄调查，随机抽取了一天40名读书者进行调查. 将他们的年龄分成6段：

    ，

    后得到如图所示的频率分布直方图，问：

    （1）在40名读书者中年龄分布在的人数；

    （2）估计40名读书者年龄的平均数和中位数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，设.

    （Ⅰ）若在处取得极值，且，求函数的单调区间；

    （Ⅱ）若时函数有两个不同的零点、.

    ①求的取值范围；②求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一元线性同余方程组问题最早可见于中国南北朝时期（公元世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：有物不知数，三三数之剩二，五五数之剩三，问物几何？即，一个整数除以三余二，除以五余三，求这个整数.设这个整数为，当时，符合条件的共有（ ）

    A. 个B. 个C. 个D. 个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中，底面是菱形，.

    （1）求证：；

    （2）若是的中点，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数 ，，已知有三个互不相等的零点，且.

    （Ⅰ）若.(ⅰ)讨论的单调区间；(ⅱ)对任意的，都有成立，求的取值范围；

    （Ⅱ）若且，设函数在，处的切线分别为直线，，是直线，的交点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面为直角梯形，，且，，，平面底面，为的中点，为等边三角形，是棱上的一点，设（与不重合）.

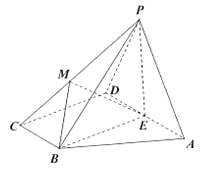
    （1）当时，求三棱锥的体积；

    （2）若平面，求的值.

    查看答案和解析>>

    同步练习册答案