
【题目】设函数 ![]() ,则关于函数f(x)有以下四个命题( )
,则关于函数f(x)有以下四个命题( )
①x∈R,f(f(x))=1;
②x0 , y0∈R,f(x0+y0)=f(x0)+f(y0);
③函数f(x)是偶函数;
④函数f(x)是周期函数.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧棱BB1⊥底面A1B1C1 , D为AC 的中点,A1B1=BB1=2,A1C1=BC1 , ∠A1C1B=60°. 
(Ⅰ)求证:AB1∥平面BDC1;
(Ⅱ)求多面体A1B1C1DBA的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.求证: 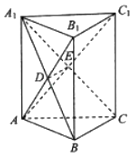
(1)DE∥平面B1BCC1;
(2)平面A1BC⊥平面A1ACC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn(n∈N*),且满足: ①|a1|≠|a2|;
②r(n﹣p)Sn+1=(n2+n)an+(n2﹣n﹣2)a1 , 其中r,p∈R,且r≠0.
(1)求p的值;
(2)数列{an}能否是等比数列?请说明理由;
(3)求证:当r=2时,数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点. 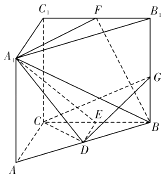
(1)当 ![]() 为何值时,平面CDG⊥平面A1DE?
为何值时,平面CDG⊥平面A1DE?
(2)求平面AB1F与平面AD1E所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)和动直线l:y=kx+b(k,b是参变量,且k≠0.b≠0)相交于A(x1 , y2),N)x2 , y2)两点,直角坐标系原点为O,记直线OA,OB的斜率分别为kOAkOB= ![]() 恒成立,则当k变化时直线l恒经过的定点为( )
恒成立,则当k变化时直线l恒经过的定点为( )
A.(﹣ ![]() p,0)
p,0)
B.(﹣2 ![]() p,0)
p,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
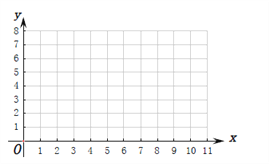
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
参考公式和数据: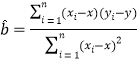 ,
,![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线![]() 上,且经过点A(-3,0),B(1,2).
上,且经过点A(-3,0),B(1,2).
(1)求圆M的方程;
(2)直线![]() 与圆M相切,且
与圆M相切,且![]() 在y轴上的截距是
在y轴上的截距是![]() 在x轴上截距的两倍,求直线
在x轴上截距的两倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com