
����Ŀ��ij���������ȡ���ָ�һѧ����������ѧ·������ʱ��Ƶ����λ:���ӣ��������������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ����������ѧ·������ʱ��ķ�Χ��![]() ���������ݷ���Ϊ
���������ݷ���Ϊ![]() .
.

(1)��ֱ��ͼ��![]() ��ֵ��
��ֵ��
(2)�����ѧ·������ʱ�䲻����1Сʱ��ѧ����������ѧУס�ޣ������� 1200��������������ж�����ѧ����������ס�ޣ�
(3)��ѧУ�ĸ�һѧ������ѡ4��ѧ������4��ѧ������ѧ·������ʱ������ 40���ӵ�������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.����ֱ��ͼ�е�Ƶ����Ϊ���ʣ�.
�ķֲ��к���ѧ����.����ֱ��ͼ�е�Ƶ����Ϊ���ʣ�.
���𰸡���1��![]() ����2��
����2��![]() ����3���ֲ��м�������
����3���ֲ��м������� ![]() .
.
�������������������1������Ƶ��ֱ��ͼ�ľ������֮��Ϊ1���x��ֵ��
��2��������ѧʱ�䲻����1Сʱ��Ƶ�ʹ���סУ������
��3�����ݶ���ֲ��ĸ��ʼ��㹫ʽ�ó��ֲ��У��ټ�����ѧ������
�������;��1����ֱ��ͼ�ɵ�![]() .
.
![]() .
.
��2��������ѧ����ʱ�䲻���ڣ�Сʱ��Ƶ��Ϊ��
![]() .
.
![]() ��������
��������
![]() ����������180��ѧ����������ס��.
����������180��ѧ����������ס��.
(3) ![]() �Ŀ���ȡֵΪ0��1��2��3��4.
�Ŀ���ȡֵΪ0��1��2��3��4.
��ֱ��ͼ��֪��ÿλѧ����ѧ����ʱ������40���ӵĸ���Ϊ![]() ,
,
![]() ��
��
![]() ��
��
![]() .
.
![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() .
.
![]() ����ѧ����Ϊ
����ѧ����Ϊ![]() .
.


 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о����ƻ����á�����ʮһ�š��ɴ������²�Ʒ����ʵ�飬�ƻ������²�Ʒ![]() ��Ҫ���ݸò�Ʒ�����Ƴɱ�����Ʒ����������ʵ����ú�Ԥ�Ʋ����������������尲�ţ�ͨ�����飬����ÿ����Ʒ�й����������
��Ҫ���ݸò�Ʒ�����Ƴɱ�����Ʒ����������ʵ����ú�Ԥ�Ʋ����������������尲�ţ�ͨ�����飬����ÿ����Ʒ�й����������
���� | ��Ʒ | ��Ʒ | ��ע |
���Ƴɱ������ط���֮��/��Ԫ | 20 | 30 | �ƻ����Ͷ�� |
���300��Ԫ��Ʒ����/ǧ�� | 10 | 5 | ������ |
����110ǧ��Ԥ������/��Ԫ | 80 | 60 | ���� |
��ʹ��Ԥ������ﵽ���ʱ�� ![]() ���ֲ�Ʒ�Ĵ��ؼ����ֱ�Ϊ(����)
���ֲ�Ʒ�Ĵ��ؼ����ֱ�Ϊ(����)
A. 9,4 B. 8,5 C. 9,5 D. 8,4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У���A��B��C��Ӧ�ı߷ֱ���a��b��c����֪cos2A��3cos��B+C��=1��
��1�����A�Ĵ�С��
��2������ABC�����S=5![]() ��b=5����sinBsinC��ֵ��
��b=5����sinBsinC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼһ������������������������һ��ֱ�������ηֱ�������ÿһ�������������ζ��õ���ͼ���ǵ�1���������������ظ�ͼ�����������õ�ͼ��Ϊ��2���������������Դ����ƣ���֪�������������Ϊ1�����![]() ���������������������εĸ���������ĺͷֱ�Ϊ�� ��
���������������������εĸ���������ĺͷֱ�Ϊ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��һ����ͼ����ͼ��ʾ������
��һ����ͼ����ͼ��ʾ������![]() ��
��![]() ��
��![]() .
.

��1������![]() ����ʽ��
����ʽ��
��2����![]() ʱ������
ʱ������![]() ��ֵ��
��ֵ��
��3��������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���ȣ��õ�����
����λ���ȣ��õ�����![]() ��ͼ������
��ͼ������![]() �ĵ����ݼ�����.
�ĵ����ݼ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��ѧ�ľ���2017�����ʡ�Ƹ��и�����ѧ����ĩ���Ե�16��) ���й�ʣ�ඨ�����ֳơ����Ӷ�����.1852��Ӣ����������ΰ���������������㾭���С��ﲻ֪��������Ľⷨ����ŷ��.1874�꣬Ӣ����ѧ������ɭָ���˷�����1801���ɸ�˹�ó��Ĺ���ͬ��ʽ�ⷨ��һ���Զ��������������֮Ϊ���й�ʣ�ඨ����. ���й�ʣ�ඨ����������һ���������������⣬��������һ���������⣺��2��2017��2016�������ܱ�3����1�ұ�5����1��������С�����˳���ų�һ�У���������![]() ��������е�����Ϊ__________��
��������е�����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������
Ϊ������ ![]() Ϊֱ�ߵ���б�ǣ���
Ϊֱ�ߵ���б�ǣ���![]() ������ԭ��
������ԭ��![]() Ϊ���㣬
Ϊ���㣬 ![]() ���������Ϊ���Ὠ��������ϵ��Բ
���������Ϊ���Ὠ��������ϵ��Բ![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .
.
��1����ֱ��![]() ����Բ
����Բ![]() ��Բ�ģ���ֱ��
��Բ�ģ���ֱ��![]() ����б�ǣ�
����б�ǣ�
��2����ֱ��![]() ��Բ
��Բ![]() ����
����![]() ��
�� ![]() ���㣬��
���㣬��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ��չ�������»����������ij����������������µ�������ʽ��Ϊ�Ƚ�����������ʽ��Ч�ʣ�ѡȡ40��������Ա������������ֳ����飬ÿ��20�ˣ���һ�鼼����Ա�õ�һ��������ʽ���ڶ��鼼����Ա�õڶ���������ʽ���������������������Ĺ���ʱ��(��λ��min)���������¾�Ҷͼ��
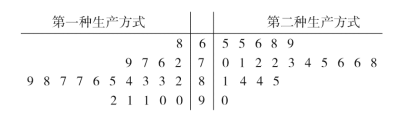
(1)��40��������Ա���������������ʱ�����λ��![]() ���������������������ʱ�䳬��
���������������������ʱ�䳬��![]() �Ͳ�����
�Ͳ�����![]() �����������������������
�����������������������
���� | ������ | �ϼ� | |
��һ��������ʽ | |||
�ڶ���������ʽ | |||
�ϼ� |
(2)����(1)�е����������ܷ���99%�İ�����Ϊ����������ʽ��Ч���в��죿
����![]()
P(K2��k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 1.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC������F��2��0��������ֱ��x=-2���У�Բ��C�Ĺ켣ΪE��
��1����Բ��C�Ĺ켣E�ķ��̣�
��2����ֱ��l��E��P��Q���㣬���߶�PQ�����ĵ����꣨1��1������|PQ|��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com