
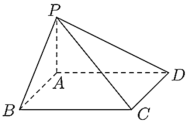
【题目】设四边形![]() 为矩形,点
为矩形,点![]() 为平面
为平面![]() 外一点,且
外一点,且![]() 平面
平面![]() ,若
,若![]() ,
,![]() .
.
(1)求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)在![]() 边上是否存在一点
边上是否存在一点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若点![]() 是
是![]() 的中点,在
的中点,在![]() 内确定一点
内确定一点![]() ,使
,使![]() 的值最小,并求此时
的值最小,并求此时![]() 的值.
的值.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)
;(3)![]() 、
、![]() 、
、![]() 三点共线,
三点共线,![]()
【解析】
(1)由题意可得:![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,可得
,可得![]() 与平面
与平面![]() 所成角既为
所成角既为![]() ,再利用解三角形的有关知识即可求出答案.
,再利用解三角形的有关知识即可求出答案.
(2)假设![]() 边上存在一点G满足题设条件,作
边上存在一点G满足题设条件,作![]() ,则
,则![]() 平面
平面![]() ,可得
,可得![]() ,进而得到
,进而得到![]() ,然后根据题意可得此点G符合题意.
,然后根据题意可得此点G符合题意.
(3)作出点C关于面PAB的对称点![]() ,连接
,连接![]() 交面PAB的点H,点H就是所求的点,再运用平面几何知识可求得HB的长.
交面PAB的点H,点H就是所求的点,再运用平面几何知识可求得HB的长.
(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,又因为底面
,又因为底面![]() 是矩形,所以
是矩形,所以![]() ,
,
所以由线面垂直的判定定理可得:![]() 平面
平面![]() ,所以
,所以![]() 与平面
与平面![]() 所成角既为
所成角既为![]() ,
,
又由题意可得:![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
(2)假设![]() 边上存在一点G满足题设条件,作
边上存在一点G满足题设条件,作![]() ,
,
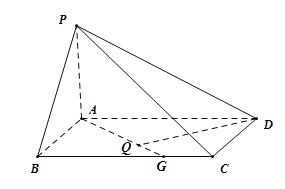
则![]() 平面
平面![]() ,
,
所以![]() .
.![]() ,
,
故存在点G,当![]() 时,使点D到平面
时,使点D到平面![]() 的距离为
的距离为![]() .
.
(3)延长CB到![]() ,使
,使![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
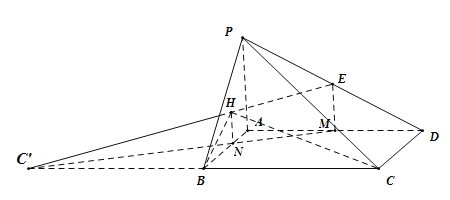
又因为底面![]() 是矩形,
是矩形,
所以![]() ,
,
所以由线面垂直的判定定理可得:![]() 平面
平面![]() ,
,
则![]() 是点C关于面
是点C关于面![]() 的对称点,
的对称点,
连接![]() ,交面
,交面![]() 于H,
于H,
则点H是使![]() 的值最小时,在面
的值最小时,在面![]() 上的一点.
上的一点.
作![]() 于M,则点M是AD的中点,连接
于M,则点M是AD的中点,连接![]() 交AB于N,连接HN,
交AB于N,连接HN,
则![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,而
,而![]() ,
,
所以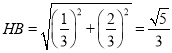 .
.
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系.直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系.直线![]() 的参数方程为
的参数方程为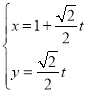 (
(![]() 为参数),圆
为参数),圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的极坐标方程;
的极坐标方程;
(2)已知点![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多边形剪一刀(截痕不过多边形的顶点)分割为![]() 个多边形,再将其中一个多边形剪一刀(截痕不过多边形的顶点)又分割出一个多边形,……如此下去。如果从一个正方形开始,要剪出一个三角形,一个四边形,一个五边形,……一个
个多边形,再将其中一个多边形剪一刀(截痕不过多边形的顶点)又分割出一个多边形,……如此下去。如果从一个正方形开始,要剪出一个三角形,一个四边形,一个五边形,……一个![]() 边形,那么,所需要剪的最少刀数为________。
边形,那么,所需要剪的最少刀数为________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从![]() 个球(其中
个球(其中![]() 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出![]() 个球(
个球(![]() ,
,![]()
![]() ),共有
),共有![]() 种取法,在这
种取法,在这![]() 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的![]() 个球全部为白球,另一类是取出1个黑球和
个球全部为白球,另一类是取出1个黑球和![]() 个白球,共有
个白球,共有![]() 种取法,即有等式
种取法,即有等式![]()
![]() 成立,试根据上述思想,化简下列式子:
成立,试根据上述思想,化简下列式子:![]() ________(
________(![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 的参数方程为:
的参数方程为:![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于A,B两点,
交于A,B两点,
![]() 求曲线
求曲线![]() 的普通方程及
的普通方程及![]() 的最小值;
的最小值;
![]() 若点
若点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷,他必选1号,不选2号,另在3至5号中随机选2名.观众乙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.
(1)求观众甲选中3号歌手的概率;
(2)![]() 表示3号歌手得到观众甲、乙的票数之和,求
表示3号歌手得到观众甲、乙的票数之和,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com