
【题目】已知函数![]()
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)令![]() ,讨论
,讨论![]() 的单调性并判断有无极值,若有,求出极值.
的单调性并判断有无极值,若有,求出极值.
【答案】(1)y=1(2)见解析
【解析】试题分析:(1)求出函数![]() 的导数,分别求出
的导数,分别求出![]() ,
, ![]() ,即可求出曲线
,即可求出曲线![]() 在点
在点![]() 处的切线方程;(2)表示出
处的切线方程;(2)表示出![]() 的表达式,求出
的表达式,求出![]() 的导数,构造
的导数,构造![]() ,可证
,可证![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,再对
,再对![]() 分类讨论,根据导数,求出单调区间,并可判断有无极值,从而求出极值.
分类讨论,根据导数,求出单调区间,并可判断有无极值,从而求出极值.
试题解析:(1)![]()
∴![]() 则切线方程为
则切线方程为![]()
(2)依题意得![]()
∴![]()
![]()
令![]() ,则
,则![]()
∴函数![]() 在R上单调递增.
在R上单调递增.
∵![]()
∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,则
,则![]() 时,
时, ![]() ,函数
,函数![]() 在(0,+∞)单调递增;
在(0,+∞)单调递增; ![]() 时,
时, ![]() ,函数
,函数![]() 在(﹣∞,0)单调递减.
在(﹣∞,0)单调递减.
∴![]() 时,函数
时,函数![]() 取得极小值,
取得极小值, ![]() ,无极大值
,无极大值
当![]() 时,令
时,令![]() ,则
,则![]() ,
, ![]()
①![]() 时,
时, ![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递增;
单调递增;
![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递增
单调递增
∴当![]() 时,函数
时,函数![]() 取得极小值,
取得极小值, ![]() .当
.当![]() 时,函数
时,函数![]() 取得极大值,
取得极大值, ![]()
![]()
②![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]()
∴函数![]() 在
在![]() 上单调递增,无极值
上单调递增,无极值
③![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递增;
单调递增;
![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,
, ![]() ,函数
,函数![]() 单调递增.
单调递增.
∴当![]() 时,函数
时,函数![]() 取得极大值,
取得极大值, ![]() ,当
,当![]() 时,函数
时,函数![]() 取得极小值,
取得极小值, ![]()
![]()
综上所述:当![]() 时,函数
时,函数![]() 在(0,+∞)单调递增,在(﹣∞,0)单调递减,
在(0,+∞)单调递增,在(﹣∞,0)单调递减, ![]() 极小值为﹣1﹣2a,无极大值;
极小值为﹣1﹣2a,无极大值;
当![]() 时,函数
时,函数![]() 在
在![]() ,(0,+∞)上单调递增,在
,(0,+∞)上单调递增,在![]() 上单调递减,
上单调递减, ![]() 极小值为
极小值为![]() ,极大值为
,极大值为![]()
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,无极值
上单调递增,无极值
当![]() 时,函数
时,函数![]() 在(﹣∞,0),
在(﹣∞,0),![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减, ![]() 极大值为
极大值为![]() .极小值为
.极小值为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
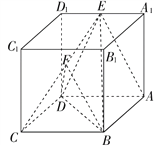
【题目】如图,正方体ABCD-A1B1C1D1中,点E是A1D1的中点,点F是CE的中点.
(Ⅰ)求证:平面ACE⊥平面BDD1B1;
(Ⅱ)求证:AE∥平面BDF.
查看答案和解析>>
科目:高中数学 来源: 题型:
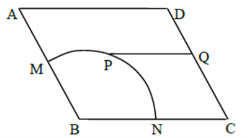
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区![]() ,其中
,其中![]() 是半径为1百米的扇形,
是半径为1百米的扇形,![]() . 管理部门欲在该地从
. 管理部门欲在该地从![]() 到
到![]() 修建小路:在弧
修建小路:在弧![]() 上选一点
上选一点![]() (异于
(异于![]() 两点),过点
两点),过点![]() 修建与
修建与![]() 平行的小路
平行的小路![]() .问:点
.问:点![]() 选择在何处时,才能使得修建的小路
选择在何处时,才能使得修建的小路![]() 与
与![]() 及
及![]() 的总长最小?并说明理由.
的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856323)已知在△ABC中,A,B,C所对的边分别为a,b,c,R为△ABC外接圆的半径,若a=1, ![]() sin2B+
sin2B+![]() sin2C-sin2A=sin Asin Bsin C,则R的值为( )
sin2C-sin2A=sin Asin Bsin C,则R的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856335)[选修4-4:坐标系与参数方程]
以原点为极点,x轴的非负半轴为极轴建立极坐标系.已知A(2,π),B(2, ![]() ),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
),圆C的极坐标方程为ρ2-6ρcos θ+8ρsin θ+21=0.F为圆C上的任意一点.
(Ⅰ)写出圆C的参数方程;
(Ⅱ)求△ABF的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
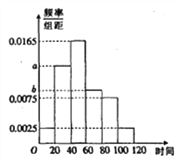
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
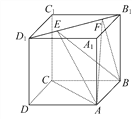
A. AC⊥BE
B. EF∥平面ABCD
C. 三棱锥A-BEF的体积为定值
D. △AEF的面积与△BEF的面积相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com