
分析 通过连结PF2、|MF2|,利用椭圆定义可知|PF1|+|PF2|=10,通过两点间距离公式计算可知|MF2|=5,利用|PM|≥|PF2|-|MF2|、|PM|≤|PF2|+|MF2|,计算即得结论.
解答 解:将M的坐标代入椭圆方程可得$\frac{36}{25}$+1>1,即M在椭圆外,
连结PF2、MF2,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的a=5,b=4,c=3,
F1(-3,0),F2(3,0),
由椭圆的定义可得,|PF1|+|PF2|=2a=10,
|MF2|=$\sqrt{(6-3)^{2}+(4-0)^{2}}$=5,
由|PM|+|PF1|≥|MF1|=$\sqrt{(6+3)^{2}+(4-0)^{2}}$=$\sqrt{97}$,
∵|PM|≤|PF2|+|MF2|,
∴|PM|+|PF1|≤|PF2|+|MF2|+|PF1|≥10+5=15,
∴|PM|+|PF1|的最大值和最小值分别为15和$\sqrt{97}$
故答案为:15,$\sqrt{97}$.
点评 本题考查椭圆的定义、方程和简单性质,考查数形结合能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
 设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).
设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
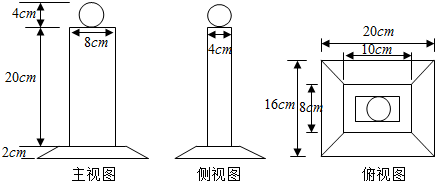
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 729 | B. | 367 | C. | 604 | D. | 854 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com