练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设y=f（x）为区间[0，1]上的连续函数，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算积分
    ∫
    1
    0
    f(x)dx    ，先产生两组（每组N个）区间[0，1]上的均匀随机数x1，x2，…xN和y1，y2，…yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方案可得积分
    ∫
    1
    0
    f(x)dx    的近似值为
     
    ．
    分析：要求∫01f（x）dx的近似值，利用几何概型求概率，结合点数比即可得．
    解答：解：由题意可知
    N1
    N
    ≈
    ∫
    1
    0
    f(x)dx
    1
    得
    ∫
    1
    0
    f(x)dx≈
    N1
    N
    ，
    故积分
    ∫
    1
    0
    f(x)dx    的近似值为
    N1
    N
    ．
    点评：本题考查几何概型模拟估计定积分值，以及定积分在面积中的简单应用，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：宁夏 题型：填空题

    设y=f（x）为区间[0，1]上的连续函数，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算积分
    ∫10
    f(x)dx    ，先产生两组（每组N个）区间[0，1]上的均匀随机数x1，x2，…xN和y1，y2，…yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方案可得积分
    ∫10
    f(x)dx    的近似值为 ______．

    查看答案和解析>>

    科目：高中数学 来源：2011年陕西省宝鸡市扶风县高考数学模拟试卷（理科）（解析版） 题型：解答题

    设y=f（x）为区间[0，1]上的连续函数，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算积分，先产生两组（每组N个）区间[0，1]上的均匀随机数x1，x2，…xN和y1，y2，…yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方案可得积分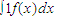的近似值为     ．

    查看答案和解析>>

    科目：高中数学 来源：2010年高考数学试卷精编：15.6 积分、行列式及矩阵（解析版） 题型：解答题

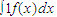    设y=f（x）为区间[0，1]上的连续函数，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算积分，先产生两组（每组N个）区间[0，1]上的均匀随机数x1，x2，…xN和y1，y2，…yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方案可得积分的近似值为     ．

    查看答案和解析>>

    科目：高中数学 来源：2010年全国统一高考数学试卷（理科）（新课标版）（解析版） 题型：解答题

    设y=f（x）为区间[0，1]上的连续函数，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算积分，先产生两组（每组N个）区间[0，1]上的均匀随机数x1，x2，…xN和y1，y2，…yN，由此得到N个点（xi，yi）（i=1，2，…，N），再数出其中满足yi≤f（xi）（i=1，2，…，N）的点数N1，那么由随机模拟方案可得积分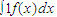的近似值为     ．

    查看答案和解析>>

    同步练习册答案