
【题目】已知椭圆![]() 的两个焦点
的两个焦点![]() ,
,![]() 与短轴的一个端点构成一个等边三角形,且直线
与短轴的一个端点构成一个等边三角形,且直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)已知过椭圆![]() 的左顶点
的左顶点![]() 的两条直线
的两条直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(3)在(2)的条件下求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)证明见;解析;定点
;(2)证明见;解析;定点![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据直线与圆相切得圆心到直线距离等于半径列一个方程,再根据等边三角形性质得![]() ,解方程组得
,解方程组得![]() ,即得结果;
,即得结果;
(2)先设直线方程,与椭圆方程联立分别解得M,N坐标,再求斜率(注意讨论),利用点斜式得直线方程,即得定点坐标;
(3)利用韦达定理以及弦长公式得![]() ,再根据三角形面积公式得
,再根据三角形面积公式得![]() 面积的函数关系式,最后根据基本不等式求最大值.
面积的函数关系式,最后根据基本不等式求最大值.
(1)由题意可得: ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的方程为:
的方程为:![]() .
.
(2)由题意知![]() ,设:
,设:![]() ,
,![]() .
.
由 消去
消去![]() 得:
得:![]() ,
,
解得:![]() 或
或![]() (舍去),
(舍去),![]() ,
,
 ,同理可得:
,同理可得: .
.
i:当![]() 时,直线
时,直线![]() 斜率存在,
斜率存在,
 ,
,
![]() ,
,![]() 直线
直线![]() 过定点
过定点![]() .
.
ii:当![]() 时,直线
时,直线![]() 斜率不存在,直线方程为:
斜率不存在,直线方程为:![]() ,也过定点
,也过定点![]() ,
,
综上所述:直线![]() 过定点
过定点![]() .
.
(3)设![]() ,由(2)知:
,由(2)知:

 ,
,
令![]() ,
, 在
在![]() 单调递减,
单调递减,
![]() ∴当
∴当![]() 时,
时, .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:
【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:

(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: ,
,![]() (回归方程
(回归方程![]() 中)
中)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是江苏卫视引进德国节目《Super Brain》而推出的大型科学竞技真人秀节目,节目筹备组透露挑选选手的方式:不但要对空间感知、照相式记忆进行考核,而且要让选手经过名校最权威的脑力测试,![]() 分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各
分以上才有机会入围,某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各![]() 名,然后对这
名,然后对这![]() 名学生进行脑力测试,规定:分数不小于
名学生进行脑力测试,规定:分数不小于![]() 分为“入围学生”,分数小于
分为“入围学生”,分数小于![]() 分为“未入围学生”,已知男生入围
分为“未入围学生”,已知男生入围![]() 人,女生未入围
人,女生未入围![]() 人,
人,
(1)根据题意,填写下面的![]() 列联表,并根据列联表判断是否有
列联表,并根据列联表判断是否有![]() 以上的把握认为脑力测试后是否为“入围学生”与性别有关.
以上的把握认为脑力测试后是否为“入围学生”与性别有关.
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | 24 | ||
女生 | 80 | ||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取![]() 名学生.
名学生.
(ⅰ)求这![]() 名学生中女生的人数;
名学生中女生的人数;
(ⅱ)若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),求这![]() 名学生中女生测试分数的平均分的最小值.
名学生中女生测试分数的平均分的最小值.
附:![]() ,其中
,其中![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,四个点
中,四个点 ,
, ,
, ,
, 中有3个点在椭圆
中有3个点在椭圆![]() :
:![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过原点的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆
不是椭圆![]() 的顶点),点
的顶点),点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,证明:存在常数
,证明:存在常数![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生活中人们常用“通五经贯六艺”形容一个人才识技艺过人,这里的“六艺”其实源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.为弘扬中国传统文化,某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“数”必须排在前两节,“礼”和“乐”必须分开安排的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比![]() .
.
(1)设圆![]() 求过
求过![]() (2,0)的直线关于圆
(2,0)的直线关于圆![]() 的距离比
的距离比![]() 的直线方程;
的直线方程;
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() (0,3)且直线
(0,3)且直线![]() =
= ![]() 关于圆
关于圆![]() 的距离比
的距离比![]() ,求此圆的
,求此圆的![]() 的方程;
的方程;
(3)是否存在点![]() ,使过
,使过![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产的某种产品中抽取1000件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
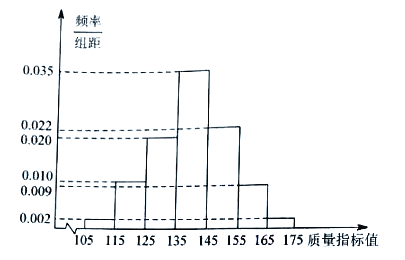
(1)求这1000件产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表)
(同一组数据用该区间的中点值作代表)
(2)由频率分布直方图可以认为,这种产品的质量指标值![]() 服从正态分布
服从正态分布![]() ,其中以
,其中以![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ⅱ)某用户从该工厂购买了100件这种产品,记![]() 表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求
表示这100件产品中质量指标值为于区间(127.6,140)的产品件数,利用(ⅰ)的结果,求![]() .
.
附:![]() .若
.若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com