[题目]已知二次函数.(1)任取.记“关于的方程有一个大于1的根和一个小于1的根为事件.求发生的概率. 题目和参考答案——青夏教育精英家教网—

【题目】已知二次函数.

（1）任取，记“关于的方程有一个大于1的根和一个小于1的根”为事件，求发生的概率.

【答案】（1）（2）

【解析】试题分析：（1）先由乘法原理确定总事件数为个，再根据条件确定且，利用枚举法确定包含事件数为5，最后根据古典概型概率求概率，（2）先作出可行域为一个直角三角形，再根据条件得，即.其可行域也是一个三角形，最后根据几何概型计算概率，测度为面积.

试题解析：解：（1）因为有3种取法，有5种取法，则对应的函数有个，

因为函数的图象关于直线对称，若事件发生，则且，

数对的取值为，，，，共5种.

所以.

（2）集合对应的平面区域为，如图，

其中点，，

则的面积为，

若事件发生，则，即.

所以事件对应的平面区域为.

由，得交点坐标为.

又，则的面积为，所以.

练习册系列答案

德华书业暑假训练营学年总复习安徽文艺出版社系列答案

金牌作业本南方教与学系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】在数列{an}中，a1=2，an+1=4an﹣3n+1，n∈N* ．
（1）证明数列{an﹣n}是等比数列；
（2）求数列{an}的前n项和Sn；
（3）证明不等式Sn+1≤4Sn ，对任意n∈N*皆成立．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数，，其中，.
（Ⅰ）若函数在处有极小值，求，的值；
（Ⅱ）若，设，求证：当时，；
（Ⅲ）若，，对于给定，，，，，其中，，，若.求的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆：的短轴长为，右焦点为，点是椭圆上异于左、右顶点的一点．

（1）求椭圆的方程；

（2）若直线与直线交于点，线段的中点为，证明：点关于直线的对称点在直线上．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】完成下列进位制之间的转化．

(1)10231(4)＝________(10)；

(2)235(7)＝________(10)；

(3)137(10)＝________(6)；

(4)1231(5)＝________(7)；

(5)213(4)＝________(3)；

(6)1010111(2)＝________(4)．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】袋子中有四个小球，分别写有“幸”“福”“快”“乐”四个字，有放回地从中任取一个小球，取到“快”就停止，用随机模拟的方法估计直到第二次停止的概率：先由计算器产生1到4之间取整数值的随机数，且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字，以每两个随机数为一组，代表两次的结果，经随机模拟产生了20组随机数：

13　24　12　32　43　14　24　32　31　21

23　13　32　21　24　42　13　32　21　34

据此估计，直到第二次就停止的概率为(　　)

A. B.

C. D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】滨湖区拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区城ABC为主题活动区，其中∠ACB=60°，∠ABC=45°，AB=12 m；AD、CD为游客通道（不考虑宽度），且∠ADC=120°，通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．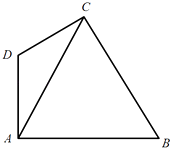

（1）求AC的长度；
（2）记游客通道AD与CD的长度和为L，求L的最大值．