
【题目】已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 最小值为0,若存在,求出
最小值为0,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是 .(填序号)
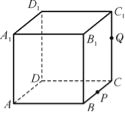
①当0<CQ<![]() 时,S为四边形;
时,S为四边形;
②当CQ=![]() 时,S为等腰梯形;
时,S为等腰梯形;
③当CQ=![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R=![]() ;
;
④当![]() <CQ<1时,S为六边形;
<CQ<1时,S为六边形;
⑤当CQ=1时,S的面积为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 和圆
和圆![]() .
.

(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() 是,求直线
是,求直线![]() 的方程;
的方程;
(2)设![]() 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点![]() 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线![]() 和
和![]() ,它们分别与圆
,它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 与被圆
与被圆![]() 截得的弦长与直线
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水尤为突出.某市为了制定合理的节水方案,从该市随机调查了100位居民,获得了他们某月的用水量,整理得到如图的频率分布直方图.
(1)求图中![]() 的值;
的值;
(2)设该市有500万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由:
(3)估计本市居民的月用水量平均数(同一组中的数据用该区间的中点值代表).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的一系列对应值如表:
)的一系列对应值如表:

(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果:
①当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围;
的取值范围;
②若![]() ,
,![]() 是锐角三角形的两个内角,试比较
是锐角三角形的两个内角,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.

(1)求![]() ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取![]() 个元件,元件寿命落在
个元件,元件寿命落在![]() 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在![]() 之间的元件中任取
之间的元件中任取![]() 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在![]() 之间,一个元件寿命落在
之间,一个元件寿命落在![]() 之间”的概率.
之间”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校随机抽取20个班,调查各班中有网上购物经历的人数,所得数据的茎叶图如图所示.以组距为5将数据分组成[0,5),[5,10),…,[30,35),[35,40]时,所作的频率分布直方图是( )
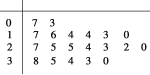

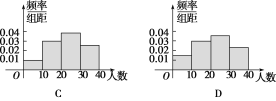
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:

(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,从这5人中再随机抽取3人赠送200元的护肤品套装,求这3人中“微信控”的人数为2的概率.
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com