
【题目】如图,在Rt△AOB中, ![]() ,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,
,斜边AB=4,D是AB中点,现将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°, 
(1)求圆锥的侧面积;
(2)求直线CD与平面BOC所成的角的大小;(用反三角函数表示)
【答案】
(1)解:∵在Rt△AOB中, ![]() ,斜边AB=4,D是AB中点,
,斜边AB=4,D是AB中点,
将Rt△AOB以直角边AO为轴旋转一周得到一个圆锥,点C为圆锥底面圆周上一点,且∠BOC=90°,
∴圆锥的侧面积S侧=πrl=2×4×π=8π
(2)解:取OB的中点E,连结DE、CE,

则DE∥AO,∴DE⊥平面BOC,
∴∠DCE是直线CD与平面BOC所成的角,
在Rt△DEC中,CE= ![]() ,DE=
,DE= ![]() ,
,
tan ![]() =
= ![]() ,
,
∴ ![]() .
.
∴直线CD与平面BOC所成角的大小为arctan ![]() .
.
【解析】(1)由圆锥的侧面积S侧=πrl,能求出结果.(2)取OB的中点E,连结DE、CE,则DE∥AO,∴DE⊥平面BOC,∠DCE是直线CD与平面BOC所成的角,由此能求出直线CD与平面BOC所成角的大小.
【考点精析】通过灵活运用空间角的异面直线所成的角,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当|a|≤1,|x|≤1时,关于x的不等式|x2﹣ax﹣a2|≤m恒成立,则实数m的取值范围是( )
A.[ ![]() ,+∞)
,+∞)
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
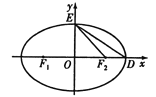
【题目】如图![]() 为椭圆C:
为椭圆C:![]()
![]() 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率![]() ,
,![]() 的面积为
的面积为![]() .若点
.若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线![]() 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点![]() 的直线
的直线![]() ,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三边长构成公差为d(d≠0)的等差数列,则△ABC最大内角α的取值范围为( )
A.![]() <α≤
<α≤ ![]()
B.![]() <α<π
<α<π
C.![]() ≤α<π
≤α<π
D.![]() <α≤
<α≤ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(x∈R)(其中A>0,ω>0,0<φ<![]() )的周期为π,且图象上一个最低点为M(
)的周期为π,且图象上一个最低点为M(![]() ,﹣2)
,﹣2)
(1)求f(x)的解析式
(2)求f(x)的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com