
分析 (1)通过函数的导数判断f′(x)>0解得x>1,求出函数f(x)的单调递增区间;
(2)条件转化为${g^'}(x)=3{x^2}-\frac{a}{x}-9≤0$在[$\frac{1}{2}$,2]上恒成立,得到a≥[h(x)]max($x∈[\frac{1}{2},2]$),通过h(x)=3x3-9x,h′(x)=9x2-9,利用函数的单调性以及函数的最值求解即可.
解答 解:(1)根据条件${f^'}(x)=3{x^2}-\frac{3}{x}=\frac{{3({x^3}-1)}}{x}$,又x>0,则f′(x)>0解得x>1,
所以f(x)的单调递增区间是(1,+∞);
(2)由于函数g(x)在区间$[\frac{1}{2},2]$上单调递减,所以${g^'}(x)=3{x^2}-\frac{a}{x}-9≤0$在[$\frac{1}{2}$,2]上恒成立,
即3x3-9x≤a在$[\frac{1}{2},2]$上恒成立,则a≥[h(x)]max($x∈[\frac{1}{2},2]$),其中h(x)=3x3-9x,h′(x)=9x2-9,则h(x)在$[\frac{1}{2},1]$上单减,在[1,2]上单增,$a≥{[h(x)]_{max}}=max\{h(\frac{1}{2}),h(2)\}=6$,经检验,a的取值范围是[6,+∞).
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{9}$ | B. | -1 | C. | 1 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ②④ | D. | ①③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x>0,使得(x+1)ex>1” | B. | “x>0,总有(x+1)ex≥1” | ||
| C. | “x>0,使得(x+1)ex≤1” | D. | x>0,总有(x+1)ex<1” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
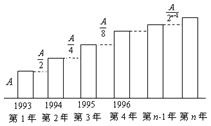 甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:
甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com