分析:(1)由于点B
1(1,y
1),B
2(2,y
2),…B
n(n,y
n)(n∈N
*)在直线
y=x+1上,可得
yn=n+1,从而可得
yn+1-yn=,从而可证
(2)已知由
=n可得x
n+x
n+1=2n,x
n+1+x
n+2=2(n+1),两式相减,得x
n+2-x
n=2,则可得奇数项和偶数项分别成等数列,由等差数列的通项公式可求x
2n-1,x
2n,进而可得|A
2n-1A
2n|=2(1-a),|A
2nA
2n+1|=2a,
yn=n+1,代入三角形的面积公式可求
解答:解:(1)由于点B
1(1,y
1),B
2(2,y
2),…B
n(n,y
n)(n∈N
*)在直线
y=x+1上,
则
yn=n+1 (2分)
因此
yn+1-yn=,
∴数列{y
n}是等差数列 (4分)
(2)已知由
=n那么x
n+x
n+1=2n (5分)
x
n+1+x
n+2=2(n+1),
以上两式相减,得x
n+2-x
n=2 (6分)
∴x
1,x
3,x
5,…,x
2n-1,…成等差数列,x
2,x
4 ,x
6,…,x
2n,…也成等数列,
∴x
2n-1=x
1+2(n-1)=2n+a-2 (7分)
∴x
2n=x
2+2(n+1)=(2-a)+2(n-1)=2n-a(9分)
∴点A
2n-1(2n+a-2,0)A
2n(2n-a,0),
则|A
2n-1A
2n|=2(1-a),|A
2nA
2n+1|=2a,
yn=n+1∴S
2n-1=
×2(1-a)×y2n-1=(1-a)×y
2n-1=
(12分)
点评:本题主要考查了等差数列的定义的应用,数列的递推公式的应用及三角形的面积公式的应用,属于知识的综合应用.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案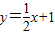 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn, 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与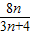 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.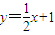 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn, 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.