
【题目】已知{an}是等差数列,其中a10=30,a20=50.
(1)求数列{an}的通项公式;
(2)若bn=an﹣20,求数列{bn}的前n项和Tn的最小值.
【答案】
(1)解:由a10=30,a20=50,
得: ![]() ,解得a1=12,d=2,
,解得a1=12,d=2,
∴an=2n+10;
(2)解:由bn=an﹣20,得bn=2n﹣10,
数列{bn}为首项﹣8,公差为2的等差数列,
∴当n<5时,bn<0;当n>5时,bn>0;当n=5时,bn=0,
由此可知:数列{bn}的前4或5项的和最小,
又T4=T5=﹣20,数列{bn}的前n项和的最小值为﹣20.
【解析】(1)根据等差数列的通项公式列出等式,解出a1和d,即可得到通项公式,(2)由(1)得出bn的通项公式,不难得出数列{bn}为首项﹣8,公差为2的等差数列,当n<5时,bn<0;当n>5时,bn>0;当n=5时,bn=0,即数列{bn}的前4或5项的和最小,由求和公式即可求出最小值.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系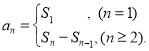 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a2=6,a3+a4=72.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an﹣n(n∈N*),求数列{bn}的前n项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项为正数的等比数列,{bn}是等差数列,且a1=b1=1,b2+b3=2a3 , a5﹣3b2=7.
(1)求{an}和{bn}的通项公式;
(2)设cn=anbn , n∈N* , 求数列{cn}的前n项和为Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1 , y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F2、F1是双曲线 ![]() =1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
=1(a>0,b>0)的上、下焦点,点F2关于渐近线的对称点恰好落在以F1为圆心,|OF1|为半径的圆上,则双曲线的离心率为( )
A.3
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是计算1 ![]() 的值的程序框图,则图中①、②处应填写的语句分别是( )
的值的程序框图,则图中①、②处应填写的语句分别是( )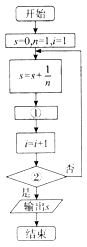
A.n=n+2,i>10?
B.n=n+2,i≥10?
C.n=n+1,i>10?
D.n=n+1,i≥10?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 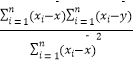 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)在[﹣3,3]上是奇函数,且对任意x,y都有f(x+y)=f(x)+f(y),当x>0时,f(x)<0,f(1)=﹣2:
(Ⅰ)求f(2)的值;
(Ⅱ)判断f(x)的单调性,并证明你的结论;
(Ⅲ)求不等式f(x﹣1)>4的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三边所在直线方程:lAB:3x﹣2y+6=0,lAC:2x+3y﹣22=0,lBC:3x+4y﹣m=0(m∈R,m≠30).
(1)判断△ABC的形状;
(2)当BC边上的高为1时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com