
【题目】设![]() .若满射
.若满射![]() ,满足:对任意的
,满足:对任意的![]() ,
,![]() ,则称
,则称![]() 为“和谐函数”.记
为“和谐函数”.记 ![]() ,
,![]() .设“和谐映射”
.设“和谐映射”![]() 为满足条件:存在正整数
为满足条件:存在正整数![]() ,使得(1)当
,使得(1)当![]() 时,若
时,若![]() ,
,![]() ,则
,则![]()
![]()
![]() ;(2)若
;(2)若![]() ,
,![]() ,则
,则![]() ,求
,求![]() 的最大可能值.
的最大可能值.
【答案】1008
【解析】
一方面,注意到2017为素数.
设![]() 为模2017的一个原则,则
为模2017的一个原则,则![]() 关于模2017的半阶为1008.
关于模2017的半阶为1008.
令![]() .
.
因为![]() ,所以,
,所以,![]() 遍历模2017的完系.
遍历模2017的完系.
于是,映射![]() 为满射.
为满射.
又![]() ,即
,即
![]() ,
,
故这样定义的![]() 为“和谐映射”.
为“和谐映射”.
据![]() 的定义知
的定义知![]() .
.
此时,由![]() ,得
,得![]()
![]() .
.
注意到,![]() 关于模2017的半阶为1008.
关于模2017的半阶为1008.
故![]() .
.
从而,所求的![]() .
.
另一方面,作凸2017边形![]() ,记作图
,记作图![]() .
.
按如下规则连线:若![]() ,
,![]() ,则连线段
,则连线段![]() .
.
显然,所连线段为图![]() 的对角线,且所连的线段没有重复.否则,若存在两条连线相同,即存在
的对角线,且所连的线段没有重复.否则,若存在两条连线相同,即存在![]() ,及
,及![]() ,使得
,使得![]() ,且
,且![]() 或
或![]() .
.
则![]() .
.
注意到,![]() ,这与题设条件矛盾.故所连对角线没有重复.
,这与题设条件矛盾.故所连对角线没有重复.
因为共连有![]() 条线段,而凸2017边形
条线段,而凸2017边形![]() 共有2017×2017条线段,
共有2017×2017条线段,
所以,![]() .
.
综上,所求![]() 的最大值为1008.
的最大值为1008.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
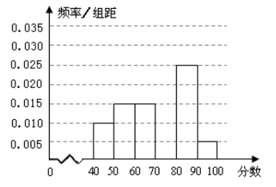
(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱柱![]() 中,底面边长为
中,底面边长为![]() ,侧棱长为
,侧棱长为![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值;
所成的角的正弦值;
(3)设![]() 为截面
为截面![]() 内-点(不包括边界),求
内-点(不包括边界),求![]() 到面
到面![]() ,面
,面![]() ,面
,面![]() 的距离平方和的最小值.
的距离平方和的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左顶点
,左顶点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若以
两点,若以![]() 为直径的圆经过坐标原点,证明:
为直径的圆经过坐标原点,证明:![]() 到直线
到直线![]() 的距离为定值.
的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查患胃病是否与生活不规律有关,在患胃病与生活不规律这两个分类变量的计算中,下列说法正确的是( )
A.![]() 越大,“患胃病与生活不规律没有关系”的可信程度越大.
越大,“患胃病与生活不规律没有关系”的可信程度越大.
B.![]() 越大,“患胃病与生活不规律有关系”的可信程度越小.
越大,“患胃病与生活不规律有关系”的可信程度越小.
C.若计算得![]() ,经查临界值表知
,经查临界值表知![]() ,则在
,则在![]() 个生活不规律的人中必有
个生活不规律的人中必有![]() 人患胃病.
人患胃病.
D.从统计量中得知有![]() 的把握认为患胃病与生活不规律有关,是指有
的把握认为患胃病与生活不规律有关,是指有![]() 的可能性使得推断出现错误.
的可能性使得推断出现错误.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com