
各项均为正数的数列{an}中,设 ,
, ,且
,且 ,
, .
.
(1)设 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合 .
.
(1)详见解析,(2)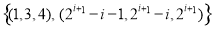 (
(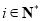 ).
).
【解析】
试题分析:(1)数列{bn}是等比数列,实际就是证明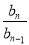 为常数,首先列出
为常数,首先列出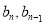 的关系式,由
的关系式,由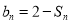 知消去参数
知消去参数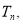 由
由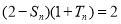 ,所以
,所以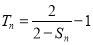 ①,当
①,当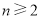 时,
时,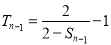 ②,①-②,得
②,①-②,得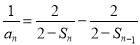 即
即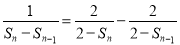 ,
,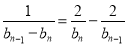 ,化简得
,化简得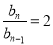 或
或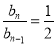 (
(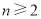 ).因为数列{an}的各项均为正数,所以数列
).因为数列{an}的各项均为正数,所以数列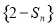 单调递减,所以
单调递减,所以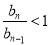 .所以
.所以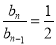 (
(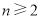 ).
).
(2)由(1)知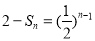 ,所以
,所以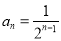 ,即
,即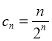 .由
.由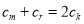 ,得
,得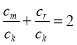 ,又
,又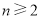 时,
时,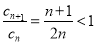 ,所以数列
,所以数列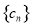 从第2项开始依次递减.当
从第2项开始依次递减.当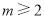 时,若
时,若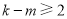 ,则
,则 ,与
,与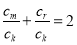 矛盾,所以
矛盾,所以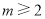 时,
时, ,即
,即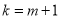 .令
.令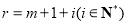 ,则
,则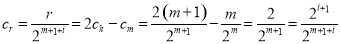 ,所以
,所以 ,即存在满足题设的数组
,即存在满足题设的数组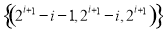 (
(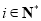 ).当
).当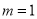 时,若
时,若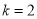 ,则
,则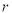 不存在;若
不存在;若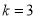 ,则
,则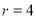 ;若
;若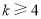 时,
时,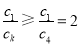 ,(*)式不成立.
,(*)式不成立.
【解】(1)当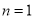 时,
时,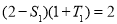 ,
,
即 ,解得
,解得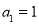 . 2分
. 2分
由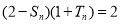 ,所以
,所以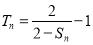 ①
①
当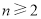 时,
时,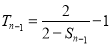 ②
②
①-②,得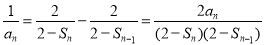 (
(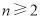 ), 4分
), 4分
即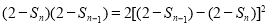 ,
,
即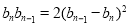 ,所以
,所以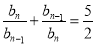 ,
,
因为数列{an}的各项均为正数,所以数列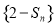 单调递减,所以
单调递减,所以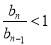 .
.
所以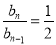 (
(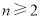 ).
).
因为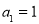 ,所以
,所以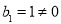 ,
,
所以数列{bn}是等比数列. 6分
(2)由(1)知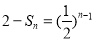 ,所以
,所以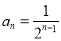 ,即
,即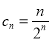 .
.
由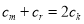 ,得
,得 (*)
(*)
又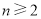 时,
时,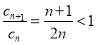 ,所以数列
,所以数列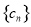 从第2项开始依次递减. 8分
从第2项开始依次递减. 8分
(Ⅰ)当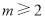 时,若
时,若 ,则
,则 ,
,
(*)式不成立,所以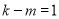 ,即
,即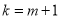 . 10分
. 10分
令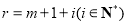 ,则
,则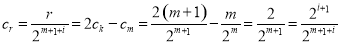 ,
,
所以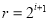 ,即存在满足题设的数组
,即存在满足题设的数组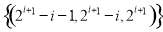 (
(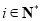 ). 13分
). 13分
(Ⅱ)当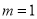 时,若
时,若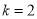 ,则
,则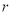 不存在;若
不存在;若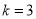 ,则
,则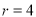 ;
;
若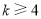 时,
时,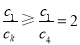 ,(*)式不成立.
,(*)式不成立.
综上所述,所求集合为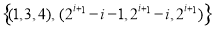 (
(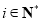 ). 16分
). 16分
(注:列举出一组给2分,多于一组给3分)
考点:数列的通项公式、前n项和


科目:高中数学 来源:2013-2014学年江苏省高考模拟考试理科数学试卷(解析版) 题型:解答题
给定椭圆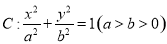 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为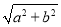 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是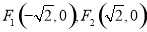 .
.
(1)若椭圆C上一动点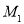 满足
满足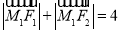 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点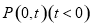 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为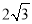 ,求P点的坐标;
,求P点的坐标;
(3)已知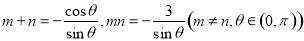 ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点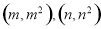 的直线的最短距离
的直线的最短距离 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,设动点P,Q都在曲线C: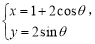 (θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.
(θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,已知定点F(1,0),点
中,已知定点F(1,0),点 在
在 轴上运动,点
轴上运动,点 在
在 轴上,点
轴上,点
为平面内的动点,且满足 ,
, .
.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)设点 是直线
是直线 :
: 上任意一点,过点
上任意一点,过点 作轨迹
作轨迹 的两条切线
的两条切线 ,
, ,切点分别为
,切点分别为 ,
, ,设切线
,设切线 ,
, 的斜率分别为
的斜率分别为 ,
, ,直线
,直线 的斜率为
的斜率为 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
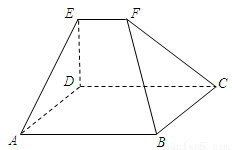
(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:填空题
已知函数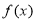 对任意的
对任意的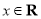 满足
满足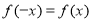 ,且当
,且当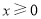 时,
时,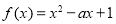 .若
.若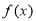 有4个零点,则实数
有4个零点,则实数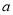 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:解答题
袋中装有大小和形状相同的小球若干个黑球和白球,且黑球和白球的个数比为4:3,从中任取2个球都是白球的概率为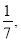 现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
(1)求袋中原有白球、黑球的个数;
(2)求随机变量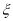 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com