
分析 建立坐标系,取曲线上任意一点(x,y)(y>0),利用曲线上的每一点到l的距离与这点到点F(0,2)的距离的差是2,可得方程,化简可得曲线的方程.
解答 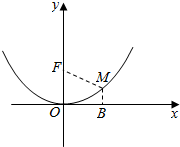 解:(1)以直线l所在直线为x轴,过F与l垂直的直线为y轴,则F(0,2)
解:(1)以直线l所在直线为x轴,过F与l垂直的直线为y轴,则F(0,2)
取曲线上任意一点M(x,y)(y>0)
∵曲线上的每一点到x轴的距离与这点到点F(0,2)的距离的差是2,
∴$\sqrt{{x}^{2}+(y-2)^{2}}$-y=2
∴x2=8y(y>0).
(2)以过F与l垂直的直线为y轴,过F与y轴垂直的直线为x轴,则F(0,0)
,l:y=-2,
取曲线上任意一点M(x,y)
∵曲线上的每一点到y=-2的距离减去这点到点F(0,0)的距离的差是2,
∴$\sqrt{{x}^{2}+{y}^{2}}$=y+4
∴x2=8(y+2).
点评 求曲线的轨迹方程是解析几何的两个基本问题之一,求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系,本题利用直接法求解,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
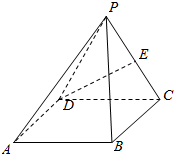 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
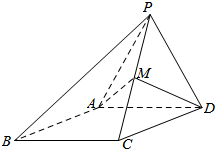 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com