
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
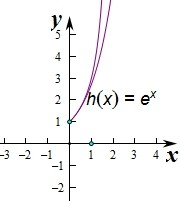 解:①当a=b=0时.满足(
解:①当a=b=0时.满足(| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| x+2 |
| 2-x |
| 4 |
| x-4 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:山东省诸城市2012届高三10月月考数学理科试题 题型:013
以下有关命题的说法错误的是
A.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”
B.“x=1”是“x2-3x+2=0”的充分不必要条件
C.若p∧q为假命题,则p、q均为假命题
D.对于命题p:![]() x∈R,使得x2+x+1<0,则
x∈R,使得x2+x+1<0,则![]() p:
p:![]() x∈R,均有x2+x+1≥0
x∈R,均有x2+x+1≥0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川眉山市高三上学期一诊测理科数学试卷(解析版) 题型:填空题
对于以下命题
①若 =
= ,则a>b>0;
,则a>b>0;
②设a,b,c,d是实数,若a2+b2=c2+d2=1,则abcd的最小值为 ;
;
③若x>0,则((2一x)ex<x+2;
④若定义域为R的函数y=f(x),满足f(x)+ f(x+2)=2,则其图像关于点(2,1)对称。
其中正确命题的序号是_______(写出所有正确命题的序号)。
查看答案和解析>>
科目:高中数学 来源: 题型:
对于以下命题:①若![]() ~
~![]() ②若
②若![]() ~
~![]() ③在某项测量中,测 量结果
③在某项测量中,测 量结果![]() 服从正态分布N
服从正态分布N![]() (0,2)内取值的概率为0.8,则
(0,2)内取值的概率为0.8,则![]() 在(0,1)内取值的概率为0.4其中正确的命题有
在(0,1)内取值的概率为0.4其中正确的命题有
A.①② B.②③ C.①③ D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com