
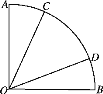
【题目】如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
根据题意得到试验的全部结果所构成的区域为Ω={(x,y)|0≤x≤90,0≤y≤90},事件A表示∠AOC+∠BOD<45°,则其所构成的区域为A={(x,y)|x+y<45,0≤x≤90,0≤y≤90},由几何概型的公式得到概率P(A)=![]()

设∠AOC=x°,∠BOD=y°,把(x,y)看作坐标平面上的点,则试验的全部结果所构成的区域为Ω={(x,y)|0≤x≤90,0≤y≤90},若事件A表示∠AOC+∠BOD<45°,则其所构成的区域为A={(x,y)|x+y<45,0≤x≤90,0≤y≤90},即图中的阴影部分,故面积S阴影=![]() ×45×45.由几何概型的概率公式,得所求概率P(A)=
×45×45.由几何概型的概率公式,得所求概率P(A)=![]()
故答案为:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1 , x2∈[0,2]且x1≠x2时,都有 ![]() <0,给出下列四个命题:
<0,给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为增函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx3+3(k﹣1)x2﹣k2+1在x=0,x=4处取得极值.
(1)求常数k的值;
(2)求函数f(x)的单调区间与极值;
(3)设g(x)=f(x)+c,且x∈[﹣1,2],g(x)≥2c+1恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图所示,已知成绩在130~140分数段的人数为2.
(1)求这组数据的平均数M.
(2)现根据初赛成绩从第一组和第五组(从低分段至高分段依次为第一组、第二组、…、第五组)中任意选出两人,形成帮扶小组.若选出的两人的成绩之差大于20,则称这两人为“黄金搭档组”,试求选出的两人为“黄金搭档组”的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+bln(x+1)在[0,+∞)上单调递减,则b的取值范围( )
A.[0,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣∞,0]
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)若函数f(x)在区间(a,a+ ![]() )(a>0)上存在极值点,求实数a的取值范围;
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
(Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.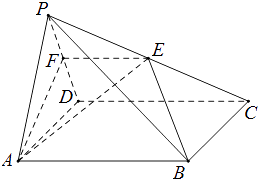
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com