
【题目】在![]() 中,
中, ![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,求
的中点,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知,利用正弦定理可得![]() a2=
a2=![]() b2+
b2+![]() c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
c2-2b,再利用余弦定理即可得出cosA,结合A的范围即可得解A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
试题解析:
(1)因为![]() asin A=(
asin A=(![]() b-c)sin B+(
b-c)sin B+(![]() c-b)·sin C,
c-b)·sin C,
由正弦定理得![]() a2=(
a2=(![]() b-c)b+(
b-c)b+(![]() c-b)c,
c-b)c,
整理得![]() a2=
a2=![]() b2+
b2+![]() c2-2bc,
c2-2bc,
由余弦定理得cos A=![]() =
=![]() =
=![]() ,
,
因为A∈(0,π),所以A=![]() .
.
(2)由cos B=![]() ,得sin B=
,得sin B=![]() =
=![]() =
=![]() ,
,
所以cos C=cos[π-(A+B)]=-cos(A+B)=-![]() =-
=-![]() ,
,
由正弦定理得b=![]() =
=![]() =2,
=2,
所以CD=![]() AC=1,
AC=1,
在△BCD中,由余弦定理得BD2=(![]() )2+12-2×1×
)2+12-2×1×![]() ×
×![]() =13,
=13,
所以BD=![]() .
.


科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和是Sn , 若点An(n, ![]() )在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
)在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
(1)求数列{an}的通项公式;
(2)记bn=a ![]() ,求数列{bn}的前n项和Tn的最小值.
,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金![]() 的关系式分别为
的关系式分别为![]() ,其中
,其中![]() 为常数且
为常数且![]() .设对乙种产品投入奖金
.设对乙种产品投入奖金![]() 百万元,其中
百万元,其中![]() .
.
(1)当![]() 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益![]() 最大;(总收益
最大;(总收益![]() )
)
(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公差不为0的等差数列![]() 中,已知
中,已知![]() 且
且![]() ,其前
,其前![]() 项和
项和![]() 的最大值为( )
的最大值为( )
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】设等差数列![]() 的公差为
的公差为![]() ,
,
∵![]() ,
,
∴![]() ,
,
整理得![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴当![]() 时,
时, ![]() .
.
故![]() 最大,且
最大,且![]() .选B.
.选B.
点睛:求等差数列前n项和最值的常用方法:
①利用等差数列的单调性, 求出其正负转折项,便可求得和的最值;
②将等差数列的前n项和![]() (A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
(A、B为常数)看作关于n的二次函数,根据二次函数的性质求最值.
【题型】单选题
【结束】
9
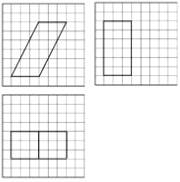
【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
A. ![]() B.
B. ![]() C. 90 D. 81
C. 90 D. 81
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种,则该网店
①第一天售出但第二天未售出的商品有______种;
②这三天售出的商品最少有_______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点. 
(1)证明PA∥平面BDE;
(2)证明:DE⊥面PBC;
(3)求直线AB与平面PBC所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com