
【题目】共享单车是城市交通的一道亮丽的风景,给人们短距离出行带来了很大的方便.某校”单车社团”对![]() 市年龄在
市年龄在![]() 岁骑过共享单车的人群随机抽取
岁骑过共享单车的人群随机抽取![]() 人调查,骑行者的年龄情况如下图显示。
人调查,骑行者的年龄情况如下图显示。
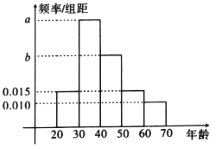
(1)已知![]() 年龄段的骑行人数是
年龄段的骑行人数是![]() 两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;
两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;
(2)从![]() 两个年龄段骑过共享单车的人中按
两个年龄段骑过共享单车的人中按![]() 的比例用分层抽样的方法抽取
的比例用分层抽样的方法抽取![]() 人,从中任选
人,从中任选![]() 人,求两人都在
人,求两人都在![]() )的概率.
)的概率.
 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
【题目】某校学生研究学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设![]() 表示学生注意力指标.
表示学生注意力指标.
该小组发现![]() 随时间
随时间![]() (分钟)的变化规律(
(分钟)的变化规律(![]() 越大,表明学生的注意力越集中)如下:
越大,表明学生的注意力越集中)如下: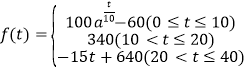 (
(![]() 且
且![]() ).
).
若上课后第![]() 分钟时的注意力指标为
分钟时的注意力指标为![]() ,回答下列问题:
,回答下列问题:
(![]() )求
)求![]() 的值.
的值.
(![]() )上课后第
)上课后第![]() 分钟和下课前
分钟和下课前![]() 分钟比较,哪个时间注意力更集中?并请说明理由.
分钟比较,哪个时间注意力更集中?并请说明理由.
(![]() )在一节课中,学生的注意力指标至少达到
)在一节课中,学生的注意力指标至少达到![]() 的时间能保持多长?
的时间能保持多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为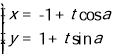 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在函数
在函数![]() 的图象上,数列
的图象上,数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(![]() )求数列
)求数列![]() 的通项公式.
的通项公式.
(![]() )设
)设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .求数列
.求数列![]() 的前
的前![]() 项和
项和![]() .
.
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() 是定义在正整数集上的函数,对于任意的正整数
是定义在正整数集上的函数,对于任意的正整数![]() ,
,![]() ,恒有
,恒有![]() 成立,且
成立,且![]() (
(![]() 为常数,
为常数,![]() ),试判断数列
),试判断数列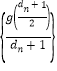 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,动点满足
,动点满足![]() 成等差数列。
成等差数列。
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)对于![]() 轴上的点
轴上的点![]() ,若满足
,若满足![]() ,则称点
,则称点![]() 为点
为点![]() 对应的“比例点”,问:对任意一个确定的点
对应的“比例点”,问:对任意一个确定的点![]() ,它总能对应几个“比例点”?
,它总能对应几个“比例点”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 的左焦点为
的左焦点为![]() ,且过点
,且过点 .
.

(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线![]() 与椭圆E交于
与椭圆E交于![]() 两点,与
两点,与![]() 的交点为
的交点为![]() ,且满足.
,且满足. ![]()
![]()
①若![]() ,求:
,求: ![]() 的值;
的值;
②设点![]() 是椭圆E的左顶点,点
是椭圆E的左顶点,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,试探究:在线段
,试探究:在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得直线
,使得直线![]() 过定点
过定点![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标;如果不存在,请说明理由。
的坐标;如果不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次足球比赛共12支球队参加,分三个阶段进行.
(1)小组赛:经抽签分成甲、乙两组,每组6队进行单循环比赛,以积分及净剩球数取前两名;
(2)半决赛:甲组第一名与乙组第二名,乙组第一名与甲组第二名作主客场交叉淘汰赛(每两队主客场各赛一场)决出胜者;
(3)决赛:两个胜队参加决赛一场,决出胜负.
问全程赛程共需比赛多少场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某单位用2160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为![]() 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为![]() (单位:元).
(单位:元).
(1)写出楼房每平方米的平均综合费用![]() 关于建造层数
关于建造层数![]() 的函数关系式;
的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com