
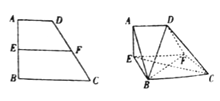
【题目】如图,在直角梯形![]() 中,
中,![]() ,且
,且![]() 分别为线段
分别为线段![]() 的中点,沿
的中点,沿![]() 把
把![]() 折起,使
折起,使![]() ,得到如下的立体图形.
,得到如下的立体图形.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学参加比赛,只有其中三位获奖.甲说:“乙或丙未获奖”;乙说:“甲、丙都获奖”;丙说:“我未获奖”;丁说:“乙获奖”.四位同学的话恰有两句是对的,则( )
A. 甲和乙不可能同时获奖 B. 丙和丁不可能同时获奖
C. 乙和丁不可能同时获奖 D. 丁和甲不可能同时获奖
【答案】C
【解析】若甲乙丙同时获奖,则甲丙的话错,乙丁的话对;符合题意;
若甲乙丁同时获奖,则乙的话错,甲丙丁的话对;不合题意;
若甲丙丁同时获奖,则丙丁的话错,甲乙的话对;符合题意;;
若丙乙丁同时获奖,则甲乙丙的话错,丁的话对;不合题意;
因此乙和丁不可能同时获奖,选C.
【题型】单选题
【结束】
12
【题目】已知当![]() 时,关于
时,关于![]() 的方程
的方程![]() 有唯一实数解,则
有唯一实数解,则![]() 值所在的范围是( )
值所在的范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,写出
,写出![]() 的单调递增区间(直接写结果)
的单调递增区间(直接写结果)
(2)若![]() ,设
,设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
参考结论:函数![]() (
(![]() 为常数),
为常数),![]() 时,
时,![]() 在
在![]() 上递增;
上递增;![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 上递增.
上递增.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量主要受污染物排放量及大气扩散等因素的影响,某市环保监测站2014年10月连续10天(从左到右对应1号至10号)采集该市某地平均风速及空气中氧化物的日均浓度数据,制成散点图如图所示.
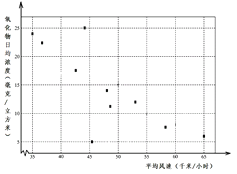
(Ⅰ)同学甲从这10天中随机抽取连续5天的一组数据,计算回归直线方程.试求连续5天的一组数据中恰好同时包含氧化物日均浓度最大与最小值的概率;
(Ⅱ)现有30名学生,每人任取5天数据,对应计算出30个不同的回归直线方程.已知30组数据中有包含氧化物日均浓度最值的有14组.现采用这30个回归方程对某一天平均风速下的氧化物日均浓度进行预测,若预测值与实测值差的绝对值小于2,则称之为“拟合效果好”,否则为“拟合效果不好”.根据以上信息完成下列2×2联表,并分析是否有95%以上的把握说拟合效果与选取数据是否包含氧化物日均浓度最值有关.
预测效果好 | 拟合效果不好 | 合计 | |
数据有包含最值 | 5 | ||
数据无包含最值 | 4 | ||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
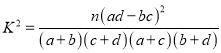 (其中
(其中![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为创建国家级文明城市,某城市号召出租车司机在高考期间至少参加一次“爱心送考”,该城市某出租车公司共200名司机,他们参加“爱心送考”的次数统计如图所示.
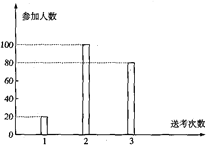
(1)求该出租车公司的司机参加“爱心送考”的人均次数;
(2)从这200名司机中任选两人,设这两人参加送考次数之差的绝对值为随机变量![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.

(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地公共电汽车和地铁按照里程分段计价,具体如下表:
乘公共电汽车方案 | 10公里(含)内2元; 10公里以上部分,每增加1元可乘坐5公里(含) |
乘坐地铁方案 | 6公里(含)内3元; 6公里至12公里(含)4元; 12公里至22公里(含)5元; 22公里至32公里(含)6元; 32公里以上部分,每增加1元可乘坐20公里(含) |
已知在一号线地铁上,任意一站到![]() 站的票价不超过5元,现从那些只乘坐一号线地铁,且在
站的票价不超过5元,现从那些只乘坐一号线地铁,且在![]() 站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
站出站的乘客中随机选出120人,他们乘坐地铁的票价统计如图所示.
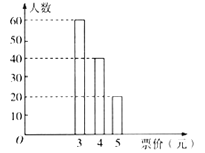
(Ⅰ)如果从那些只乘坐一号线地铁,且在![]() 站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
站出站的乘客中任选1人,试估计此人乘坐地铁的票价小于5元的概率;
(Ⅱ)已知选出的120人中有6名学生,且这6名学生中票价为3、4、5元的人数分别为3,2,1人,现从这6人中随机选出2人,求这2人的票价和恰好为8元的概率;
(Ⅲ)小李乘坐一号线地铁从![]() 地到
地到![]() 站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为
站的票价是5元,返程时,小李乘坐某路公共电汽车所花交通费也是5元,假设小李往返过程中乘坐地铁和公共电汽车的路程均为![]() 公里,试写出
公里,试写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com