
| 3 |
| 4 |
| C | 3 5 |
| C | 1 2 |
| •C | 2 5 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 256 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 256 |
| 3+9 |
| 256 |
| 3 |
| 64 |
| 3 |
| 64 |


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
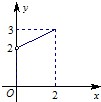 已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.
已知函数f(x)是定义在[-2,0)∪(0,2]上的奇函数,当x>0时,f(x)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| m2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| ||
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 10 |
| MF1 |
| MF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下:
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左向右滚下,最后掉入编号为1,2,…,7的球槽内.某高三同学试验1000次,掉入各球槽的个数统计如下:| 球槽 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 频数 | 15 | 95 | x | y | 234 | 92 | 17 |
| 频率 | 0.015 | 0.095 | 0.234 | z | 0.234 | 0.092 | 0.017 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com