已知函数f(x)=x3-ax2-bx+a2,x∈R,a,b为常数.
(1)若函数f(x)在x=1处有极值10,求实数a,b的值;
(2)若函数f(x)是奇函数,
①方程f(x)=2在x∈[-2,4]上恰有3个不相等的实数解,求实数b的取值范围;
②不等式f(x)+2b≥0对?x∈[1,4]恒成立,求实数b的取值范围.
分析:(1)求出函数的导函数,令导函数在x=1的值为0,令函数在x=1的值10,列出方程组,求出a,b的值,将求出的a,b值代入导函数,判断是否在x=0取得极值.
(2)①构造新函数,求出新函数的导数,通过对b的讨论,判断出函数的单调性,求出函数的极值,据方程根的个数,判断出极值的符号,列出不等式求出b的范围.
②通过对x的分段讨论分离出b,构造函数,通过导数求出函数的最值,求出b的范围.
解答:解:(1)f′(x)=3x
2-2ax-b,
由f(x)在x=1处有极值10,得f’(1)=0,f(1)=10.
即3-2a-b=0,1-a-b+a?2=10,
解得a=3,b=-3或a=-4,b=11.
经检验,a=3,b=-3不合题意,舍去.
∴a=-4,b=11.
(2)由于函数f(x)的定义域为R,
由函数f(x)是奇函数,得f(0)=0,
∴a=0.
①由f(x)=2,得f(x)-2=0,
令g(x)=f(x)-2=x
3-bx-2,
则方程g(x)=0在x∈[-2,4]上恰有3个不相等的实数解.
∵g′(x)=3x
2-b,
(ⅰ)若b≤0,则g′(x)≥0恒成立,且函数g(x)不为常函数,
∴g(x)在区间[-2,4]上为增函数,g(0)=0,
所以,g(x)=0在区间[-2,4]上有且只有一个实数解.
不合题意,舍去.
(ⅱ)若b>0,则函数g(x)在区间(-∞,-
)上为增函数,在区间(-,
)上为减函数,
在区间(
,+∞)上为增函数,
由方程g(x)=0在x∈[-2,4]上恰有3个不相等的实数解,
可得
解得
∴b∈(3,5]
②由不等式f(x)+2b≥0,得x
3-bx+2b≥0,即(x-2)b≤x
3,
(ⅰ)若x-2=0即x=2时,b∈R;
(ⅱ)若x-2<0即x∈[1,2)时,b≥
在区间[1,2)上恒成立,
令h(x)=
,则b≥h(x)
max.
∵h′(x)=
,
∴h′(x)<0在x∈[1,2)上恒成立,
所以h(x)在区间[1,2)上是减函数,
∴h(x)
max=h(1)=-1,
∴b≥-1.
(ⅲ)若x-2>0即x∈(2,4]时,b≤
在区间(2,4]上恒成立,则b≤h(x)
min.
由(ⅱ)可知,函数所以h(x)在区间(2,3)上是减函数,在区间(3,4]上是增函数,
∴h(x)
min=h(3)=27,
∴b≤27.
综上所述,b∈[-1,27].
点评:解决函数的极值问题要注意:极值点处的导数值为0是函数取得极值的必要不充分条件;解决不等式恒成立问题常采用分离参数转化为求函数的最值.



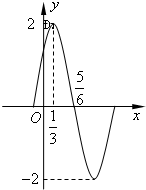 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<