
分析 (1)建立坐标系,然后,分别写出相关点的坐标,然后,根据向量的数量积运算,计算即可说明成立;
(2)首先,设出P(2,y),Q(x-2,t),则2x=4-ty,再结合0≤x≤2,得到?y∈[0,t],都有0≤4-ty≤4,只需要t≤($\frac{4}{m}$)min,即可确定t的取值范围.
解答 解:(1)如下图所示: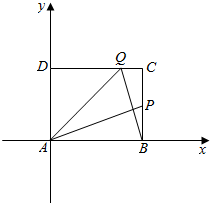
设点A(0,0),B(2,0),C(2,t),D(0,t),P(2,y0),Q(x0,t),
∴$\overrightarrow{AP}$=(2,y0),$\overrightarrow{BQ}$=(x0-2,t),
∴$\overrightarrow{AP}•\overrightarrow{BQ}$=2x0-4+ty0=0,
∴2x0+ty0=4,
∵$\overrightarrow{AQ}$=(x0,t),
∴$\overrightarrow{AP}•\overrightarrow{AQ}$=2x0+ty0=4(定值),
∴$\overrightarrow{AP}$•$\overrightarrow{AQ}$为定值.
(2)P(2,y),Q(x-2,t),则2x=4-ty,
∵0≤x≤2,
∴?y∈[0,t],都有0≤4-ty≤4,即0≤ty≤4,
当y=0时,t∈R,
当0<y≤t时,mt≤4,t≤$\frac{4}{m}$,
∴t≤($\frac{4}{m}$)min,
∴t≤$\frac{4}{t}$,即0≤t≤2.
点评 本题重点考查了向量的坐标表示、向量的基本运算等知识,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:填空题
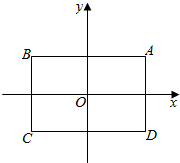 如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.
如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分是点A,B的对应点,$\frac{A′B′}{AB}$=k.已知关于x,y的元二次一次方程$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$(m,n是实数)无解,在以m,n为坐标(记为m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上.则k•t的值等于1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com