练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，曲线C的极坐标方程为ρ2cos2θ+3ρ2sin2θ=3，直线l的参数方程为 ．试在曲线C上求一点M，使它到直线l的距离最大．

    【答案】解：曲线C的普通方程是 ．

    直线l的普通方程是 ．

    设点M的坐标是 的距离是 ．

    ，

    d取得最大值．

    ．


    【解析】将曲线C，直线l的极坐标方程化为普通方程，设出点M的坐标，利用点到直线的距离公式表示出点M到直线l的距离d，再利用三角函数求得d最大值及此时点M的坐标.
    【考点精析】认真审题，首先需要了解点到直线的距离公式(点到直线的距离为：)，还要掌握直线的参数方程(经过点，倾斜角为的直线的参数方程可表示为（为参数）)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，若输出的S的值为64，则判断框内可填入的条件是（ ）
    A.k≤3？
    B.k＜3？
    C.k≤4？
    D.k＞4？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（　　）
    A.命题“x∈R，使得x2+x+1＜0”的否定是：“x∈R，x2+x+1＞0”
    B.命题“若x2﹣3x+2=0，则x=1或x=2”的否命题是：“若x2﹣3x+2=0，则x≠1或x≠2”
    C.直线l1：2ax+y+1=0，l2：x+2ay+2=0，l1∥l2的充要条件是
    D.命题“若x=y，则sinx=siny”的逆否命题是真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校举行“庆元旦”教工羽毛球单循环比赛（任意两个参赛队只比赛一场），共有高一、高二、高三三个队参赛，高一胜高二的概率为 ，高一胜高三的概率为 ，高二胜高三的概率为P，每场胜负独立，胜者记1分，负者记0分，规定：积分相同者高年级获胜．
    （Ⅰ）若高三获得冠军概率为 ，求P．
    （Ⅱ）记高三的得分为X，求X的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PC⊥平面ABCD，AB∥CD，CD⊥AC，过CD的平面分别与PA，PB交于点E，F．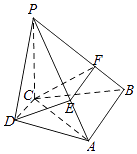

    （1）求证：CD⊥平面PAC；
    （2）求证：AB∥EF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若Sn为等差数列{an}的前n项和，且a1=1，S10=55．记bn=[lnan]，其中[x]表示不超过x的最大整数，如[0.9]=0，[lg99]=1．则数列{bn}的前2017项和为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=lnx+ax2（a∈R），y=f（x）的图象连续不间断．
    （1）求函数y=f（x）的单调区间；
    （2）当a=1时，设l是曲线y=f（x）的一条切线，切点是A，且l在点A处穿过函数y=f（x）的图象（即动点在点A附近沿曲线y=f（x）运动，经过点A时，从l的一侧进入另一侧），求切线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图扇形AOB是一个观光区的平面示意图，其中∠AOB的圆心角为 ，半径OA为1Km，为了便于游客观光休闲，拟在观光区内铺设一条从入口A到出口B的观光道路，道路由圆弧AC、线段CD及线段BD组成．其中D在线段OB上，且CD∥AO，设∠AOC=θ，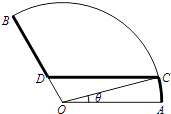

    （1）用θ表示CD的长度，并写出θ的取值范围．
    （2）当θ为何值时，观光道路最长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆 的左、右焦点分别为F1（﹣c，0）、F2（c，0），过椭圆中心的弦PQ满足|PQ|=2，∠PF2Q=90°，且△PF2Q的面积为1．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）直线l不经过点A（0，1），且与椭圆交于M，N两点，若以MN为直径的圆经过点A，求证：直线l过定点，并求出该定点的坐标．

    查看答案和解析>>

    同步练习册答案