
【题目】已知f(x)=![]() .
.
(1)若f(x)>k的解集为{x|x<﹣3或x>﹣2},求k的值;
(2)若对任意x>0,f(x)≤t恒成立,求实数t的取值范围.
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在平行于OA的直线![]() ,使得直线
,使得直线![]() 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与![]() 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D﹣ABC中,已知△BCD是正三角形,平面ABC⊥平面BCD,AB=BC=a,AC= ![]() a,E为BC的中点,F在棱AC上,且AF=3FC.
a,E为BC的中点,F在棱AC上,且AF=3FC. 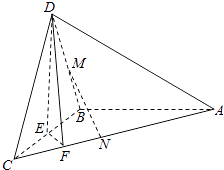
(1)求三棱锥D﹣ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN= ![]() CA,求证:MN∥平面DEF.
CA,求证:MN∥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() ,直线
,直线![]() 与
与
圆![]() 相切,且直线
相切,且直线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]()
相交于![]() 两点,
两点, ![]() 为原点。
为原点。
(1)若直线![]() 过椭圆
过椭圆![]() 的左焦点,且与圆
的左焦点,且与圆![]() 交于
交于![]()
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
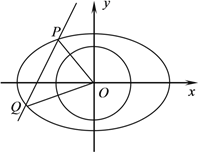
(2)如图,若![]() 的重心恰好在圆上,求
的重心恰好在圆上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)如图,椭圆![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线l的方程为
,直线l的方程为![]() .
.

(1)求椭圆C的方程;
(2)![]() 是经过右焦点
是经过右焦点![]() 的任一弦(不经过点
的任一弦(不经过点![]() ),设直线
),设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,记
,记![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() .问:是否存在常数
.问:是否存在常数![]() ,使得
,使得![]() ? 若存在,求
? 若存在,求![]() 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,直线
,直线![]() 经过点
经过点![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点.
两点.

(1)若![]() 且
且![]() ,求证:
,求证: ![]() 必为
必为![]() 的焦点;
的焦点;
(2)设![]() ,若点
,若点![]() 在
在![]() 上,且
上,且![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为坐标原点,若
为坐标原点,若![]() ,直线
,直线![]() 的一个法向量为
的一个法向量为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
按分层抽样抽取10只,再随机抽取3只品尝,记![]() 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com