
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由两条异面直线所成的角的取值范围可以判断①,由平面向量数量积的运算可以判断②,在空间,点M在平面ABC内的充要条件是存在α、β、γ,使$\overrightarrow{OM}$=α$\overrightarrow{OA}$+β $\overrightarrow{OB}$+γ$\overrightarrow{OC}$且α+β+γ=1可以判断③,由三个向量非零不共线可以判断④,从而可得到正确的命题个数.
解答 解:对于①:∵两条异面直线所成的角的取值范围是(0°,90°],
∴异面直线MN与PQ所成角的余弦值不能为负值,故①不正确;
对于②:∵$\overrightarrow{a}$•$\overrightarrow{b}$=(2,4,-3)(-1,2,2)=-2+8-6=0,
∴$\overrightarrow{a}$⊥$\overrightarrow{b}$.∴平面α与平面β垂直,故②正确;
对于③:∵$\overrightarrow{OM}=\frac{1}{5}\overrightarrow{OA}+\frac{4}{5}\overrightarrow{OB}+\frac{2}{5}\overrightarrow{BC}$,且$\frac{1}{5}+\frac{4}{5}+\frac{2}{5}=\frac{7}{5}≠1$
∴M点不在平面ABC内,故③不正确;
对于④:∵向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$是空间的一个基底,则向量$\overrightarrow a+\overrightarrow b+\overrightarrow c$、$\overrightarrow a+\overrightarrow b$、$\overrightarrow c$也是空间的一个基底,∵三个向量非零不共线,故④正确.
∴其中正确的命题个数是:2.
故选:B.
点评 本题考查了命题的真假判断与应用,考查了两条异面直线所成的角的取值范围以及平面向量数量积的运算,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (2,5) | C. | (-2,-1] | D. | (-∞,2)∪[5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
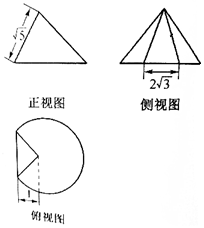 一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )| A. | $\frac{8π}{3}$+$\sqrt{15}$ | B. | $\frac{16π}{3}$+$\sqrt{3}$ | C. | $\frac{8π}{3}$+$\frac{2\sqrt{3}}{3}$ | D. | $\frac{16π}{9}$+$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
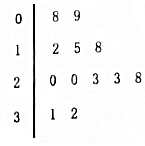 广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )
广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )| A. | 20;23 | B. | 21.5;20,23 | C. | 20;20,23 | D. | 21.5;23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $ω=2,ϕ=\frac{π}{3}$ | B. | $ω=2,ϕ=\frac{π}{6}$ | C. | $ω=4,ϕ=\frac{π}{6}$ | D. | $ω=2,ϕ=-\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com