
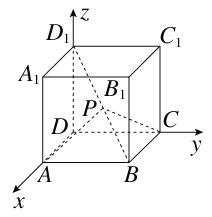
【题目】设动点P在棱长为1的正方体ABCD-A1B1C1D1的对角线BD1上,记![]() =λ.当∠APC为钝角时,λ的取值范围是________.
=λ.当∠APC为钝角时,λ的取值范围是________.
【答案】(![]() ,1)
,1)
【解析】
本题主要考查了用空间向量求直线间的夹角,一元二次不等式的解法,意在考查考生的空间想象能力以及运算求解能力.
以![]() 、
、![]() 、
、![]() 为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则
为单位正交基底,建立如图所示的空间直角坐标系D-xyz,则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),则![]() =(1,1,-1),得
=(1,1,-1),得![]() =λ
=λ![]() =(λ,λ,-λ),所以
=(λ,λ,-λ),所以![]() =
=![]() +
+![]() =(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),
=(-λ,-λ,λ)+(1,0,-1)=(1-λ,-λ,λ-1),![]() =
=![]() +
+![]() =(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于
=(-λ,-λ,λ)+(0,1,-1)=(-λ,1-λ,λ-1),显然∠APC不是平角,所以∠APC为钝角等价于![]() ·
·![]() <0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得
<0,即-λ(1-λ)-λ(1-λ)+(λ-1)2<0,即(λ-1)(3λ-1)<0,解得![]() <λ<1,因此λ的取值范围是(
<λ<1,因此λ的取值范围是(![]() ,1).
,1).


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
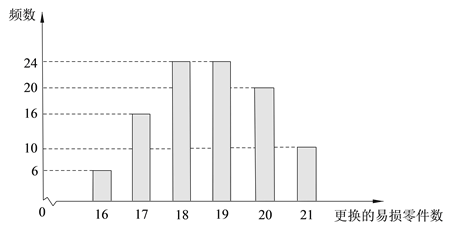
记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元), ![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(Ⅰ)若![]() =19,求y与x的函数解析式;
=19,求y与x的函数解析式;
(Ⅱ)若要求“需更换的易损零件数不大于![]() ”的频率不小于0.5,求
”的频率不小于0.5,求![]() 的最小值;
的最小值;
(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n,x的值分别为4,2,则输出v的值为 ( )
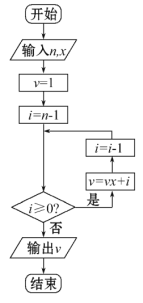
A. 9B. 18C. 25D. 50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 交
交![]() 于点
于点![]() .现将
.现将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到图2.
,得到图2.
(Ⅰ)在图2中,求证: ![]() ;
;
(Ⅱ)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在什么位置时,二面角
在什么位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班50名学生参加防疫知识竞赛,将所有成绩制作成频率分布表如下:
分组 | 频数 | 频率 |
|
|
|
|
| 0.06 |
| 35 | 0.070 |
| 6 | 0.12 |
| 4 |
|
(1)求频率分布表中![]() 的值;
的值;
(2)从成绩在![]() 的学生中选出2人,请写出所有不同的选法,并求选出2人的成绩都在
的学生中选出2人,请写出所有不同的选法,并求选出2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() 的4个交点恰为一个正方形的4个顶点.
的4个交点恰为一个正方形的4个顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点, ![]() 为椭圆
为椭圆![]() 上与
上与![]() 不重合的两点,若直线
不重合的两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,试判断是否存在定点
,试判断是否存在定点![]() ,使得直线
,使得直线![]() 恒过点
恒过点![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com