考点:二面角的平面角及求法,平面与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(Ⅰ)先由线面垂直的判定定理,得到BC⊥平面ACC
1A
1又DC
1?平面ACC
1A
1,所以DC
1⊥BC,再证得DC
1⊥DC.
再由线面垂直的判定即可得证;
(Ⅱ)分别以
,
,
为x,y,z轴建立直角坐标系,设AA
1=2,显然平面CBC
1的法向量为
=(1,0,0),设平面BC
1D的法向量为
=(x
0,y
0,z
0),由
•
=0,
•
=0,得到
=(1,2,1),再由向量的夹角公式,即可得到二面角的余弦值.
解答:
(Ⅰ)证明:由题意知BC⊥CC
1,BC⊥AC,CC
1∩AC=C,
所以BC⊥平面ACC
1A
1又DC
1?平面ACC
1A
1,所以DC
1⊥BC,
由题设知∠A
1DC
1=∠ADC=45°,
所以∠CDC
1=90°,即DC
1⊥DC.
又DC∩BC=C,所以DC
1⊥平面BDC;
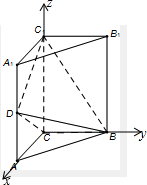
(Ⅱ)解:如图,分别以
,
,
为x,y,z轴建立直角坐标系,
设AA
1=2,显然平面CBC
1的法向量为
=(1,0,0),
设平面BC
1D的法向量为
=(x
0,y
0,z
0)
由于
=(0,0,2)-(0,1,0)=(0,1,0),
=(0,0,2)-(1,0,1)=(-1,0,1),
则由
•
=0,
•
=0
得-y
0+2z
0=0,-x
0+z
0=0,即
=(1,2,1),
由cos<
,
>=
=
,
故二面角C-BC
1-D的余弦值为
.
点评:本题考查空间直线与平面的位置关系,考查空间的二面角的求法,考查推理能力和空间向量法,及运算能力,属于中档题.

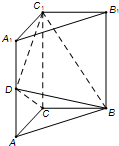 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC= (Ⅰ)证明:由题意知BC⊥CC1,BC⊥AC,CC1∩AC=C,
(Ⅰ)证明:由题意知BC⊥CC1,BC⊥AC,CC1∩AC=C,
