
【题目】已知函数![]() ,
, ![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值;
的最小值;
(3)若![]() ,正实数
,正实数![]() ,
, ![]() 满足
满足![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由![]() 求出
求出![]() 的值,再利用导数求出函数
的值,再利用导数求出函数![]() 的单调递减区间;(2)分离出变量
的单调递减区间;(2)分离出变量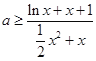 ,令
,令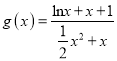 ,只要
,只要![]() ,利用导数求出令
,利用导数求出令![]() 的最大值即可;(3)由
的最大值即可;(3)由![]() ,即
,即![]() ,令
,令![]() ,则由
,则由![]() ,利用导数法求得
,利用导数法求得![]() ,从而可得所以
,从而可得所以![]() ,解得即可.
,解得即可.
试题解析:
(1)因为![]() ,所以
,所以![]() ,
,
此时![]() ,
, ![]() ,
,
![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() 的单调减区间为
的单调减区间为![]() .
.
(2)由![]() 恒成立,得
恒成立,得![]() 在
在![]() 上恒成立,
上恒成立,
问题等价于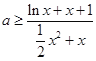 在
在![]() 上恒成立,
上恒成立,
令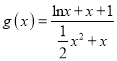 ,只要
,只要![]() ,
,
因为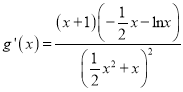 ,令
,令![]() ,得
,得![]() .
.
设![]() ,因为
,因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
不妨设![]() 的根为
的根为![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]()
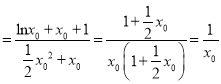 ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,此时
,此时![]() ,即
,即![]() ,
,
所以![]() ,即整数
,即整数![]() 的最小值为2.
的最小值为2.
(3)当![]() 时,
时, ![]() ,
,
由![]() ,即
,即![]() ,
,
从而![]() ,
,
令![]() ,则由
,则由![]() ,得
,得![]() ,
,
可知, ![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以![]() ,因此
,因此![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值:
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;则a=____,b=_______
(2)直线l1与直线l2平行,并且直线l2在y轴上的截距为3.则a=____,b=_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递减,在区间
单调递减,在区间![]() 单调递增.函数
单调递增.函数 .
.
(1)请写出函数![]() 与函数
与函数![]() 在
在![]() 的单调区间;(只写结论,不需证明)
的单调区间;(只写结论,不需证明)
(2)求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)讨论方程![]() 实根的个数.
实根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x﹣y=2上运动时, ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某闯关游戏规则是:先后掷两枚骰子,将此试验重复n轮,第n轮的点数分别记为xn , yn , 如果点数满足xn< ![]() ,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
,则认为第n轮闯关成功,否则进行下一轮投掷,直到闯关成功,游戏结束.
(Ⅰ)求第一轮闯关成功的概率;
(Ⅱ)如果第i轮闯关成功所获的奖金数f(i)=10000× ![]() (单位:元),求某人闯关获得奖金不超过1250元的概率;
(单位:元),求某人闯关获得奖金不超过1250元的概率;
(Ⅲ)如果游戏只进行到第四轮,第四轮后不论游戏成功与否,都终止游戏,记进行的轮数为随机变量X,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,建设生态文明是中华民族永续发展的千年大计.而清洁能源的广泛使用将为生态文明建设提供更有力的支撑.沼气作为取之不尽、用之不竭的生物清洁能源,在保护绿水青山方面具有独特功效.通过办沼气带来的农村“厕所革命”,对改善农村人居环境等方面,起到立竿见影的效果.为了积极响应国家推行的“厕所革命”,某农户准备建造一个深为2米,容积为32立方米的长方体沼气池,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,沼气池盖子的造价为3000元,问怎样设计沼气池能使总造价最低?最低总造价是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为![]() 人,每位员工的培训费为
人,每位员工的培训费为![]() 元,培训机构的利润为
元,培训机构的利润为![]() 元.
元.
(1)写出![]() 与
与![]()
![]() 之间的函数关系式;
之间的函数关系式;
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(a>b>0)的短轴长为2,过上顶点E和右焦点F的直线与圆M:x2+y2﹣4x﹣2y+4=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l过点(1,0),且与椭圆C交于点A,B,则在x轴上是否存在一点T(t,0)(t≠0),使得不论直线l的斜率如何变化,总有∠OTA=∠OTB (其中O为坐标原点),若存在,求出 t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com