
【题目】设函数f(x)在(m,n)上的导函数为g(x),x∈(m,n),g(x)若的导函数小于零恒成立,则称函数f(x)在(m,n)上为“凸函数”.已知当a≤2时, ![]() ,在x∈(﹣1,2)上为“凸函数”,则函数f(x)在(﹣1,2)上结论正确的是( )
,在x∈(﹣1,2)上为“凸函数”,则函数f(x)在(﹣1,2)上结论正确的是( )
A.既有极大值,也有极小值
B.有极大值,没有极小值
C.没有极大值,有极小值
D.既无极大值,也没有极小值
科目:高中数学 来源: 题型:
【题目】体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p (p≠0),发球次数为X,若X的数学期望EX>1.75,则p的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(0, ![]() )
)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣
(α为参数).以点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ﹣ ![]() )=2
)=2 ![]() (Ⅰ)将直线l化为直角坐标方程;
(Ⅰ)将直线l化为直角坐标方程;
(Ⅱ)求曲线C上的一点Q 到直线l 的距离的最大值及此时点Q的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= ![]() AC=2,∠ACB=∠ACD=
AC=2,∠ACB=∠ACD= ![]() .
. 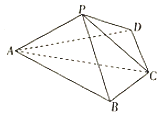
(1)证明:AP⊥BD;
(2)若AP= ![]() ,AP与BC所成角的余弦值为
,AP与BC所成角的余弦值为 ![]() ,求二面角A﹣BP﹣C的余弦值..
,求二面角A﹣BP﹣C的余弦值..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果定义在R上的函数f(x)满足:对于任意x1≠x2 , 都有xlf(xl)+x2f(x2)≥xlf(x2)+x2f(xl),则称f(x)为“H函数”,给出下列函数: ①y=﹣x3+x+l;
②y=3x﹣2(sinx﹣cosx);
③y=l﹣ex;
④f(x)= ![]() ;
;
⑤y= ![]()
其中“H函数”的个数有( )
A.3个
B.2个
C.l个
D.0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设方程(m+1)|ex﹣1|﹣1=0的两根分别为x1 , x2(x1<x2),方程|ex﹣1|﹣m=0的两根分别为x3 , x4(x3<x4).若m∈(0, ![]() ),则(x4+x1)﹣(x3+x2)的取值范围为( )
),则(x4+x1)﹣(x3+x2)的取值范围为( )
A.(﹣∞,0)
B.(﹣∞,ln ![]() )
)
C.(ln ![]() ,0)
,0)
D.(﹣∞,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在(0,+∞)的函数f(x)的导函数是f'(x),且x4f'(x)+3x3f(x)=ex , ![]() ,则x>0时,f(x)( )
,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既无极大值,又无极小值
D.既有极大值,又有极小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com