
【题目】定义在R上的函数f(x)满足:f′(x)>1﹣f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
A.{x|x>0}
B.{x|x<0}
C.{x|x<﹣1或x>1}
D.{x|x<﹣1或0<x<1}
【答案】A
【解析】解:设g(x)=exf(x)﹣ex , (x∈R),
则g′(x)=exf(x)+exf′(x)﹣ex=ex[f(x)+f′(x)﹣1],
∵f′(x)>1﹣f(x),
∴f(x)+f′(x)﹣1>0,
∴g′(x)>0,
∴y=g(x)在定义域上单调递增,
∵exf(x)>ex+2,
∴g(x)>2,
又∵g(0)=e0f(0)﹣e0=3﹣1=2,
∴g(x)>g(0),
∴x>0,
∴不等式的解集为(0,+∞)
故选:A.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
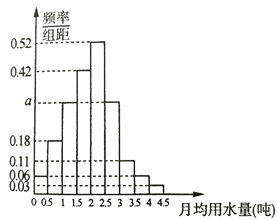
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)若将频率视为概率,从该城市居民中随机抽取3人,记这3人中月均用水量不低于3吨的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值(精确到0.01),并说明理由.
的值(精确到0.01),并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知 ![]() =(2,1),
=(2,1), ![]() =(1,7),
=(1,7), ![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点. 
(1)求使 ![]()
![]() 取最小值时的
取最小值时的 ![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
(1) 求证:直线DE∥平面A1C1F;
(2) 求证:平面B1DE⊥平面A1C1F.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的个数是( )
①若a>b,则ac2>bc2;
②若命题p为真命题题,命题q为假命题,则p∨q为假命题;
③若命题p:x0∈R,x ![]() ﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
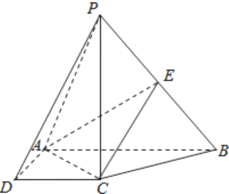
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() 是
是![]() 上的点.
上的点.
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com