
【题目】如图,在四棱锥中![]() ,底面
,底面![]() 为边长为
为边长为![]() 的正方形,
的正方形, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
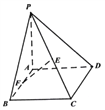
(1)求证: ![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,根据三角形中位线定理可得
,根据三角形中位线定理可得![]() ,进而得四边形
,进而得四边形![]() 为平行四边形,从而
为平行四边形,从而![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]()
![]() 平面
平面![]() ;(2)由(1)知,
;(2)由(1)知, ![]() ,因为
,因为![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,
, ![]() ,可证明
,可证明![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,向量
为坐标原点,向量![]() ,
, ![]() ,
, ![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方形建立如图所示的空间直角坐标系
轴的正方形建立如图所示的空间直角坐标系![]() ,求出直线
,求出直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,利用空间向量夹角余弦公式可得直线
的法向量,利用空间向量夹角余弦公式可得直线![]() 与平面
与平面![]() 所成角的正弦值,从而可得结果.
所成角的正弦值,从而可得结果.
试题解析:(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
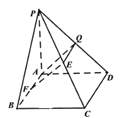
则![]() ,而
,而![]()
∴![]() ∴四边形
∴四边形![]() 为平行四边形.
为平行四边形.
∴![]() ,而
,而![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]() ;
;
(2)由(1)知, ![]() ,因为
,因为![]() 平面
平面![]()
所以![]() 平面
平面![]() ,而
,而![]() ,
, ![]()
![]() 平面
平面![]()
∴![]()
∵![]() ,
, ![]() ,
, ![]()
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() ,而
,而![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
(注意:没有证明出![]() 平面
平面![]() ,直接运用这一结论的,后续过程不给分)
,直接运用这一结论的,后续过程不给分)
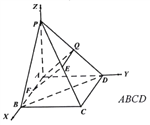
由题意, ![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,向量
为坐标原点,向量![]() ,
, ![]() ,
, ![]() 的方向为
的方向为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴的正方形建立如图所示的空间直角坐标系
轴的正方形建立如图所示的空间直角坐标系![]()
在三角形![]() 中
中![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,知
,知![]() ,而
,而![]() 的中点为
的中点为![]() 知
知![]() ,则
,则![]() ,
, ![]() ,
, 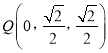 ,
, ![]() ,
, ![]()
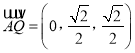 ,
, ![]() ,
, ![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
, 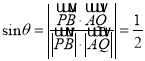
所以直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.

(1)根据频率分布直方图,估计这50名同学的数学成绩的众数;
(2)用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() .
.
(1)求实数![]() 的值,并指出函数
的值,并指出函数![]() 的定义域;
的定义域;
(2)将函数![]() 图象上的所有点向右平行移动1个单位得到函数
图象上的所有点向右平行移动1个单位得到函数![]() 的图象,写出函数
的图象,写出函数![]() 的表达式;
的表达式;
(3)对于(2)中的![]() ,关于
,关于![]() 的函数
的函数![]() 在
在![]() 上的最小值为2,求
上的最小值为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 、
、![]() 的极坐标分别为
的极坐标分别为![]() 、
、![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 和曲线
和曲线![]() 只有一个交点,求
只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018衡水金卷(二)】如图,矩形![]() 中,
中, ![]() 且
且![]() ,
, ![]() 交
交![]() 于点
于点![]() .
.
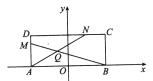
(I)若点![]() 的轨迹是曲线
的轨迹是曲线![]() 的一部分,曲线
的一部分,曲线![]() 关于
关于![]() 轴、
轴、![]() 轴、原点都对称,求曲线
轴、原点都对称,求曲线![]() 的轨迹方程;
的轨迹方程;
(II)过点![]() 作曲线
作曲线![]() 的两条互相垂直的弦
的两条互相垂直的弦![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,探究
,探究![]() 是否为定值?若是,求出此定值,若不是,请说明理由.
是否为定值?若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com