
【题目】(本小题满分14分)
已知f(x)=![]() ,x∈[1,+∞).
,x∈[1,+∞).
(1)当a=![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
【答案】(1)f(x)在[1,+∞)上的最小值为f(1)=![]() .(2)实数a的取值范围是(-3,+∞).
.(2)实数a的取值范围是(-3,+∞).
【解析】试题分析:(1)先判断函数f(x)的单调性,利用单调性求函数的最值;(2)f(x)=![]() 在区间[1,+∞)恒成立等价于
在区间[1,+∞)恒成立等价于![]() 在区间[1,+∞)恒成立,即
在区间[1,+∞)恒成立,即![]() 在区间[1,+∞)恒成立,令φ(x)=-(x2+2x)并求其在[1,+∞)上的最大值即可.
在区间[1,+∞)恒成立,令φ(x)=-(x2+2x)并求其在[1,+∞)上的最大值即可.
试题解析:
(1)当a=![]() 时,f(x)=x+
时,f(x)=x+![]() +2,任取1≤x1<x2,
+2,任取1≤x1<x2,
则f(x1)-f(x2)=(x1-x2)+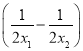 =
=![]() ,
,
∵1≤x1<x2,∴x1x2>1,∴2x1x2-1>0.
又x1-x2<0,∴f(x1)<f(x2),
∴f(x)在[1,+∞)上是增函数,
∴f(x)在[1,+∞)上的最小值为f(1)=![]() .
.
(2)在区间[1,+∞)上,f(x)=![]() 恒成立,
恒成立,
则![]()
 等价于a大于函数φ(x)=-(x2+2x)在[1,+∞)上的最大值.
等价于a大于函数φ(x)=-(x2+2x)在[1,+∞)上的最大值.
只需求函数φ(x)=-(x2+2x)在[1,+∞)上的最大值.
φ(x)=-(x+1)2+1在[1,+∞)上递减,
∴当x=1时,φ(x)最大值为φ(1)=-3.
∴a>-3,故实数a的取值范围是(-3,+∞).


科目:高中数学 来源: 题型:
【题目】某商品最近30天的价格f(t)(元)与时间t满足关系式:f(t)=  ,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C为△ABC的三内角,且其对边分别为a、b、c,若acosC+ccosA=﹣2bcosA.
(1)求角A的值;
(2)若a=2 ![]() ,b+c=4,求△ABC的面积.
,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一同学在电脑中打出如下若干个圆:○●○○●○○○●○○○○●○○○○○●…,若依此规律继续下去,得到一系列的圆,则在前2012个圆中共有●的个数是( )
A.61
B.62
C.63
D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 
A.点H是△A1BD的垂心
B.AH垂直平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|﹣1≤x≤2},B={x|x2﹣(2m+1)x+2m<0}.
(1)当m< ![]() 时,把集合B用区间表达;
时,把集合B用区间表达;
(2)若A∪B=A,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知c>0,设命题p:函数y=cx为减函数;命题q:当x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com