
【题目】在平面直角坐标系xOy中,已知圆C:![]() 及点
及点![]() ,
,![]() .
.
![]() 过B作直线l与圆C相交于M,N两点,
过B作直线l与圆C相交于M,N两点,![]() ,求直线l的方程;
,求直线l的方程;
![]() 在圆C上是否存在点P,使得
在圆C上是否存在点P,使得![]() ?若存在,求点P的个数;若不存在,说明理由.
?若存在,求点P的个数;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() 经过点
经过点![]() ,与x轴正半轴交于点B.
,与x轴正半轴交于点B.
![]() Ⅰ
Ⅰ![]() ______;
______;![]() 将结果直接填写在答题卡的相应位置上
将结果直接填写在答题卡的相应位置上![]()
![]() Ⅱ
Ⅱ![]() 圆O上是否存在点P,使得
圆O上是否存在点P,使得![]() 的面积为15?若存在,求出点P的坐标;若不存在,说明理由.
的面积为15?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=﹣sin(ωx+φ)(ω>0,φ∈(﹣ ![]() ,
, ![]() ))的一条对称轴为x=
))的一条对称轴为x= ![]() ,一个对称中心为(
,一个对称中心为( ![]() ,0),在区间[0,
,0),在区间[0, ![]() ]上单调.
]上单调.
(1)求ω,φ的值;
(2)用描点法作出y=sin(ωx+φ)在[0,π]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin(2x+ ![]() ),若将它的图象向右平移
),若将它的图象向右平移 ![]() 个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 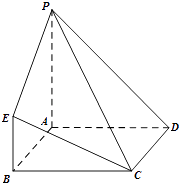
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com