
【题目】已知函数![]() ,
,
(Ⅰ)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(Ⅱ)若对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)证明![]()
科目:高中数学 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态,一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:车辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量 | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() ,
, ![]() 称为相应于点
称为相应于点![]() 的残差(也叫随机误差));
的残差(也叫随机误差));
租用单车数量 | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本 | 3.2 | 2 | 1.9 | 1.7 | ||
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 |
| 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
, ![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放,根据市场调查,这个城市投放8千辆时,该公司平均一辆单一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.4,0.6,问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入—成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式x2+(a﹣1)x+a2<0的解集是空集,命题q:已知二次函数f(x)=x2﹣mx+2满足 ![]() ,且当x∈[0,a]时,最大值是2,若命题“p且q”为假,“p或q”为真,求实数a的取值范围.
,且当x∈[0,a]时,最大值是2,若命题“p且q”为假,“p或q”为真,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() ,动点
,动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设轨迹![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 作不与
作不与![]() 轴重合的直线交轨迹
轴重合的直线交轨迹![]() 于两点
于两点![]() ,直线
,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() .试问:在
.试问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出定点
?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若以曲线![]() 上任意一点
上任意一点![]() 为切点作切线
为切点作切线![]() ,曲线上总存在异于
,曲线上总存在异于![]() 的点
的点![]() ,以点
,以点![]() 为切点作切线
为切点作切线![]() ,且
,且![]() ,则称曲线
,则称曲线![]() 具有“可平行性”,现有下列命题:
具有“可平行性”,现有下列命题:
①函数![]() 的图象具有“可平行性”;
的图象具有“可平行性”;
②定义在![]() 的奇函数
的奇函数![]() 的图象都具有“可平行性”;
的图象都具有“可平行性”;
③三次函数![]() 具有“可平行性”,且对应的两切点
具有“可平行性”,且对应的两切点![]() ,
, ![]() 的横坐标满足
的横坐标满足![]() ;
;
④要使得分段函数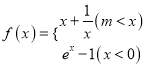 的图象具有“可平行性”,当且仅当
的图象具有“可平行性”,当且仅当![]() .
.
其中的真命题个数有()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},满足d>0,且a1+a2+a3=9,a1a3=5
(1)求{an}的通项公式;
(2)若数列{bn}满足bn= ![]() ,Sn为数列{bn}的前n项和,证明:Sn<3.
,Sn为数列{bn}的前n项和,证明:Sn<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知已知圆![]() 经过
经过 ![]() 、
、![]() 两点,且圆心C在直线
两点,且圆心C在直线 ![]() 上,求解:(1)圆C的方程;(2)若直线
上,求解:(1)圆C的方程;(2)若直线 ![]() 与圆
与圆 ![]() 总有公共点,求实数
总有公共点,求实数 ![]() 的取值范围.
的取值范围.
(1)求圆C的方程;
(2)若直线 ![]() 与圆
与圆 ![]() 总有公共点,求实数
总有公共点,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 ![]() (t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=
(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ= ![]()
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com