
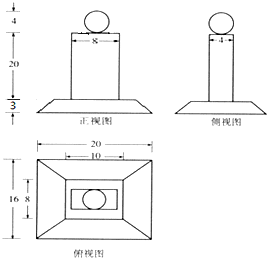
 如图是一个奖杯三视图,试根据奖杯三视图计算它的表面积与体积.(尺寸单位:cm,取$π≈3,\sqrt{34}≈6$,结果精确到整数)
如图是一个奖杯三视图,试根据奖杯三视图计算它的表面积与体积.(尺寸单位:cm,取$π≈3,\sqrt{34}≈6$,结果精确到整数) 分析 由已知中的三视图可得:该几何体由三部分组成底下几何体是四棱台,中间是四棱柱,上面是球,进而可得答案.
解答 解:底下几何体是四棱台:
求棱台的高3,正前方斜高5,左右侧面斜高$\sqrt{34}$,
下底面是长20,宽16的矩形,
上底面是长10,宽8的矩形,
中间是四棱柱,长,宽,高分别为:8,4,20,
上头是一个半径为2的球,
故几何体的表面积:
S=2×$\frac{1}{2}$(10+20)×5+2×$\frac{1}{2}$(8+16)×$\sqrt{34}$+20×16+10×8+2×(8+4)×20+4π•22=1030+24$\sqrt{34}$+16π;
几何体的体积V=$\frac{1}{3}$×(20×16+10×8+$\sqrt{20×16×10×8}$)×3+8×4×20+$\frac{4}{3}π•{2}^{3}$=1100+$\frac{32}{3}π$.
点评 本题考查的知识点是棱台的体积和表面积,棱柱的体积和表面积,球的体积和表面积,简单几何体的三视图,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 用电量(度) | (0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 户数 | 5 | 15 | 10 | 15 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com