
【题目】已知函数![]() .
.
(1)若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,
,![]() ,证明:
,证明:![]() .
.
科目:高中数学 来源: 题型:
【题目】纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形ABCD外切于![]() ,△ACB的内切圆
,△ACB的内切圆![]() 与边AB、BC的切点分别为P、Q,,△ACD的内切圆
与边AB、BC的切点分别为P、Q,,△ACD的内切圆![]() 与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
与边CD、DA的切点分别为R、S. 求证:三条直线PQ、RS、AC共点或平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(Ⅰ)求a,b的值;
(Ⅱ)讨论f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
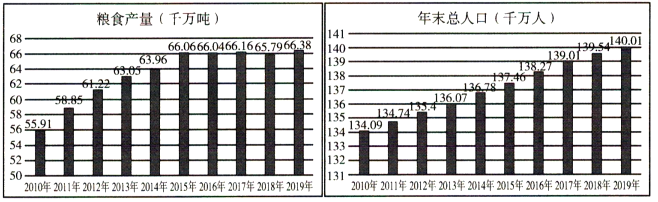
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为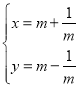 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:
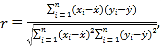
![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com