分析:由含有量词的命题的否定规则,得到①不正确;根据函数零点存在性定理,可得②是真命题;将直线l的极坐标方程化成普通方程,结合点到直线的距离公式加以验证,可得③是真命题;根据导数的运算法则与导数的几何意义,结合基本不等式求最值,可得④是真命题;根据线性回归的概念与性质,可得⑤不正确.由此可得本题的答案.
解答:解:对于①,命题的否定为“任意的x∈R,x
2-x-2<0”,所以①不正确;
对于②,因为
f(x)=x-()x,满足
f()=()-()^<0,且
f()=()-()^>0,
所以函数的零点在区间
(,),所以②是真命题;
对于③,将极坐标方程化成普通方程,得x+y-2=0,
利用点到直线的距离公式,得极点(0,0)到直线的距离为
d==
,故③是真命题;
对于④,函数f(x)=e
-x-e
x的导数为
f′(x)=-e-x-ex=-(ex+)≤-2,
当且仅当
ex=,即e
x=1,x=0时取等号,所以切线的斜率的最大值是-2,得④是真命题;
对于⑤,线性回归直线
=x+恒过样本中心
(,),但不一定过样本点,可得⑤不正确,
综上所述,得其中正确命题为②③④.
故答案为:②③④
点评:本题给出几个关于函数的零点、函数图象的切线和直线的极坐标方程的几个命题,求其中的真命题.着重考查了含有量词的命题的否定、函数零点存在性定理、导数的运算法则与几何意义和基本不等式求最值等知识,属于中档题.









 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案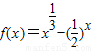 的零点在区间
的零点在区间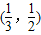 内;
内;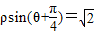 的距离是
的距离是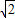 .
.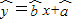 恒过样本中心
恒过样本中心 ,且至少过一个样本点.
,且至少过一个样本点.