
【题目】已知函数![]() 存在两个极值点.
存在两个极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)设![]() 和
和![]() 分别是
分别是![]() 的两个极值点且
的两个极值点且![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)对原函数求导,即该导函数在![]() 有两个不同根,对该导函数继续求导,发现只有
有两个不同根,对该导函数继续求导,发现只有![]() 一个零点,分a = 0,a < 0,a > 0三种情况讨论即可.
一个零点,分a = 0,a < 0,a > 0三种情况讨论即可.
(Ⅱ)要证![]() ,即证
,即证![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命题等价于证明![]() .
.
因为![]() ,故只需证
,故只需证![]() ,即
,即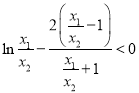
令![]() ,则
,则![]() ,设
,设![]() ,利用导数研究其单调性极值与最值即可.
,利用导数研究其单调性极值与最值即可.
试题解析:(Ⅰ)由题设函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,故函数
,故函数![]() 有两个极值点等价于其导函数
有两个极值点等价于其导函数![]() 在
在![]() 有两个零点.
有两个零点.
当a = 0时![]() ,显然只有1个零点
,显然只有1个零点![]() .当a≠0时,令
.当a≠0时,令![]() ,那么
,那么![]() .
.
若a < 0,则当x > 0时![]() ,即
,即![]() 单调递增,所以
单调递增,所以![]() 无两个零点. … 3分
无两个零点. … 3分
若a > 0,则当![]() 时
时![]() ,
, ![]() 单调递增;当
单调递增;当![]() 时
时![]() ,
, ![]() 单调递减,所以
单调递减,所以![]() . 又
. 又![]() ,当x→0时→
,当x→0时→![]() ,故若有两个零点,则
,故若有两个零点,则![]() ,得
,得![]() .
.
综上得,实数a的取值范围是![]() .
.
(Ⅱ)要证![]() ,两边同时取自然对数得
,两边同时取自然对数得![]() .
.
由![]() 得
得![]() ,得
,得![]() .
.
所以原命题等价于证明![]() .
.
因为![]() ,故只需证
,故只需证![]() ,即
,即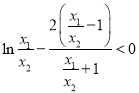
令![]() ,则
,则![]() ,设
,设![]() ,只需证
,只需证![]() .… 10分
.… 10分
而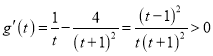 ,故
,故![]() 在
在![]() 单调递增,所以
单调递增,所以![]() .
.
综上得![]() .
.
点晴:本题主要考查函数极值,不等式证明问题.要求极值,求导得导函数,分a = 0,a < 0,a > 0三种情况讨论极值情况,要证明一个不等式,我们可以先根据题意构造新函数![]() ,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.
,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=3时,求函数f(x)的定义域;
(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;
(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=(x﹣l)(log3a)2﹣6(log3a)x+x+l在x∈[0,l]内恒为正值,则a的取值范围是( )
A.﹣1<a< ![]()
B.a< ![]()
C.a> ![]()
D.![]() <a<
<a< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若α∈[0,π],β∈[﹣ ![]() ,
, ![]() ],λ∈R,且(α﹣
],λ∈R,且(α﹣ ![]() )3﹣cosα﹣2λ=0,4β3+sinβcosβ+λ=0,则cos(
)3﹣cosα﹣2λ=0,4β3+sinβcosβ+λ=0,则cos( ![]() +β)的值为( )
+β)的值为( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合M满足M{1,2,3},且M中至少有一个奇数,这样的集合M有6个;
②已知函数f(x)= ![]() 的定义域是R,则实数a的取值范围是(﹣12,0);
的定义域是R,则实数a的取值范围是(﹣12,0);
③函数f(x)=loga(x﹣3)+1(a>0且a≠1)图象恒过定点(4,2);
④已知函数f(x)=x2+bx+c对任意实数t都有f(3+t)=f(3﹣t),则f(1)>f(4)>f(3).
其中正确的命题序号是(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com