
【题目】某市对各老旧小区环境整治效果进行满意度测评,共有10000人参加这次测评(满分100分,得分全为整数).为了解本次测评分数情况,从中随机抽取了部分人的测评分数进行统计,整理见下表:
组别 | 分组 | 频数 | 频率 |
1 |
| 3 | 0.06 |
2 |
| 15 | 0.3 |
3 |
| 21 |
|
4 |
| 3 | 0.12 |
5 |
|
| 0.1 |
合计 |
| 1.00 | |
(1)求出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若分数在80(含80分)以上表示对该项目“非常满意”,其中分数在90(含90分)以上表示“十分满意”,现从被抽取的“非常满意“人群中随机抽取2人,求至少有一人分数是“十分满意”的概率;
(3)请你根据样本数据估计全市的平均测评分数
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】本市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼.摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:
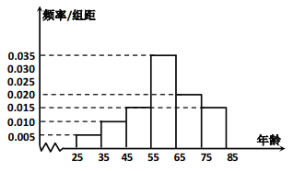
(1)根据频率分布直方图,求这100位摄影者年龄的样本平均数![]() 和中位数
和中位数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中评出20个最佳作品,并邀请作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组应抽取的人数;
年龄 |
|
|
|
|
|
|
人数 |
②若从较年轻的前三组作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,曲线![]() :
: ![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求出曲线![]() 、
、![]() 的参数方程;
的参数方程;
(Ⅱ)若![]() 、
、![]() 分别是曲线
分别是曲线![]() 、
、![]() 上的动点,求
上的动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①任意两条直线都可以确定一个平面;②若两个平面有3个不同的公共点,则这两个平面重合;③直线a,b,c,若a与b共面,b与c共面,则a与c共面;④若直线l上有一点在平面α外,则l在平面α外.其中错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .平面
.平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.
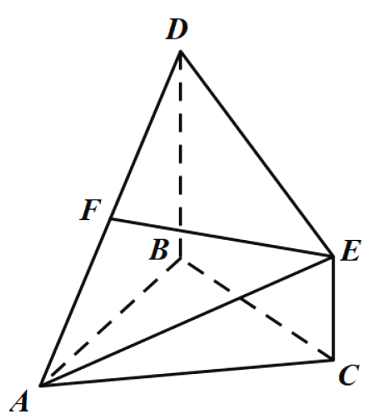
(1)求证:![]() 平面ABC;
平面ABC;
(2)求证:平面![]() 平面ABD.
平面ABD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数y=f(x),部分x与y的对应关系如表:
x | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 0 | 2 | 3 | 2 | 0 | ﹣1 | 0 | 2 |
(1)求f{f[f(0)]};
(2)数列{xn}满足x1=2,且对任意n∈N*,点(xn,xn+1)都在函数y=f(x)的图象上,求x1+x2+…+x4n;
(3)若y=f(x)=Asin(ωx+φ)+b,其中A>0,0<ω<π,0<φ<π,0<b<3,求此函数的解析式,并求f(1)+f(2)+…+f(3n)(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于曲线![]() :
:![]() 的下列说法:①关于原点对称;②关于直线
的下列说法:①关于原点对称;②关于直线![]() 对称;③是封闭图形,面积大于
对称;③是封闭图形,面积大于![]() ;④不是封闭图形,与圆
;④不是封闭图形,与圆![]() 无公共点;⑤与曲线D:
无公共点;⑤与曲线D:![]() 的四个交点恰为正方形的四个顶点,其中正确的个数是( )
的四个交点恰为正方形的四个顶点,其中正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面内互不平行的三个向量,
是平面内互不平行的三个向量,![]() ,有下列命题:
,有下列命题:
①方程![]() 不可能有两个不同的实数解;
不可能有两个不同的实数解;
②方程![]() 有实数解的充要条件是
有实数解的充要条件是![]() ;
;
③方程![]() 有唯一的实数解
有唯一的实数解![]() ;
;
④方程![]() 没有实数解.
没有实数解.
其中真命题有 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
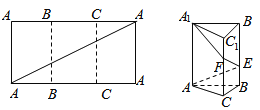
【题目】如图,把长为6,宽为3的矩形折成正三棱柱![]() ,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱
,三棱柱的高度为3,矩形的对角线和三棱柱的侧棱![]() 的交点记为E,F.
的交点记为E,F.
(1)求三棱柱![]() 的体积;
的体积;
(2)求三棱柱中异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com